CoordinateGeometry

Question 1:

Exercise 6A

Draw the perpendiculars from the AF, BG, CH, DI and EJ on the x-axis.

1. The distance of A from the y-axis = OF = -6 units The distance of A from the x-axis = AF = 5 units Hence, the coordinate of A are (-6, 5)
2. The distance of B from the y-axis = OG = 5 units The distance of B from the x-axis = BG = 4 units Hence, the coordinate of B are (5, 4)
3. The distance of C from the y-axis = OH = -3 units The distance of C from the x-axis = HC = 2 units Hence, the coordinate of C are (-3, 2)
4. The distance of D from the y-axis = OI = 2 units The distance of D from the x-axis = ID = -2 units Hence, the coordinate of D are (2, -2)
5. The distance of E from the y-axis = OJ = -1 unit The distance of E from the x-axis = JE = -4 units Hence, the coordinate of E are (-1, -4)

Thus, the coordinates of A, B, C, D and E are respectively, A(-6,5), B(5,4), C(-3,2), D(2,-2) and E(-1,-4)

Question 2:

Let X’OX and Y’OY be the coordinate axes.

Fix the side of the small squares as one units.

• 1. Starting from O, take +7 units on the x-axis and then +4 units on the y-axis to obtain the point P(7, 4)
  2. Starting from O, take -5 units on the x-axis and then +3 units on the y-axis to obtain the point Q(-5, 3)
  3. Starting from O, take -6 units on the x-axis and then -3 units on the y-axis to obtain the point R(-6, -3)
  4. Starting from O, take +3 units on the x-axis and then -7 units on the y-axis to obtain the point S(3, -7)
  5. Starting from O, take 6 units on the x-axis to obtain the point A(6, 0)
  6. Starting from O, take 9 units on the y-axis to obtain the point B(0,9)
  7. Mark the point O as O(0, 0)
  8. Starting from O, take -3 units on the x-axis and then -3 units on the y-axis to obtain the point C(-3, -3)

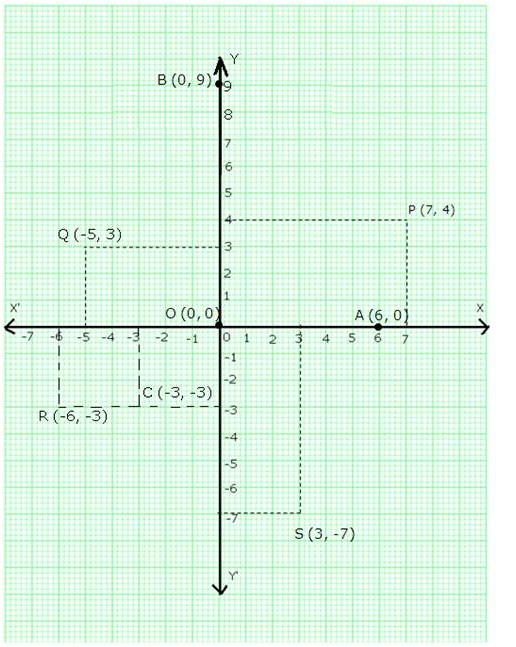
These points are shown in the following graph:

Question 3:

1. In (7, 0), we have the ordinate = 0.

Therefore, (7,0) lies on the x-axis

1. In (0, -5), we have the abscissa = 0.

Therefore, (0,-5) lies on the y-axis

1. In (0,1), we have the abscissa = 0.

Therefore, (0,1) lies on the y-axis

1. In (-4,0), we have the ordinate = 0.

Therefore, (-4,0) lies on the x-axis

Question 4:

1. Points of the type (-, +) lie in the second quadrant. Therefore, the point (-6,5) lies in the II quadrant.
2. Points of the type (-, -) lie in the third quadrant. Therefore, the point (-3,-2) lies in the III quadrant.
3. Points of the type (+, -) lie in the fourth quadrant. Therefore, the point (2,-9) lies in the IV quadrant.

Question 5:

The given equation is y = x + 1 Putting x = 1, we get y = 1 + 1 = 2

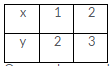
Putting x = 2, we get y = 2 + 1 = 3 Thus, we have the following table:

On a graph paper, draw the lines X’OX and YOY’ as the x-axis and y-axis respectively. Then, plot points P (1, 2) and Q (2, 3) on the graph paper. Join PQ and extend it to both sides.

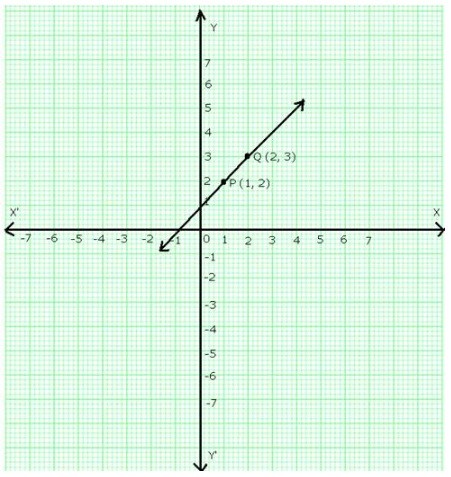
Then, line PQ is the graph of the equation y = x + 1.

Question 6:

The give equation is y = 3x + 2 Putting x = 1, we get y = (3 1) + 2 = 5

Putting x = 2, we get y = (3 2) + 2 = 8 Thus, we have the following table:

On the graph paper, draw the lines X’OX and YOY’ as the x-axis and y-axis respectively. Now, plot points P(1,5) and Q(2,8) on the graph paper.

Join PQ and extend it to both sides.

Then, line PQ is the graph of the equation y = 3x + 2.

Question 7:

The given equation is y = 5x – 3 Putting x = 0, we get y = (5 × 0) – 3 = -3

Putting x = 1, we get y = (5 × 1) – 3 = 2 Thus, we have following table:

On a graph paper, draw the lines X’OX and YOY’ as the x-axis and y-axis respectively. Now plot the points P(0,-3) and Q(1,2).

Join PQ and extend it in both the directions.

Then, line PQ is the graph of the equation, y = 5x – 3.

Question 8:

The given equation is y = 3x Putting x = 1, we get y = (3 1) = 3

Putting x = 2, we get y = (3 2) = 6 Thus, we have the following table:

On a graph paper draw the lines X’OX and YOY’ as the x-axis and y-axis respectively. Now, plot points P(1,3) and Q(2,6).

Join PQ and extend it in both the directions. Then, line PQ is the graph of the equation y = 3x.

Question 9:

The given equation is y = -x

Putting x = 1, we get y = -1 Putting x = 2, we get y = -2

Thus, we have the following table:

On a graph paper, draw the lines X’OX and YOY’ as the x-axis and y-axis respectively. Now, plot the points P(1,-1) and Q(2,-2).

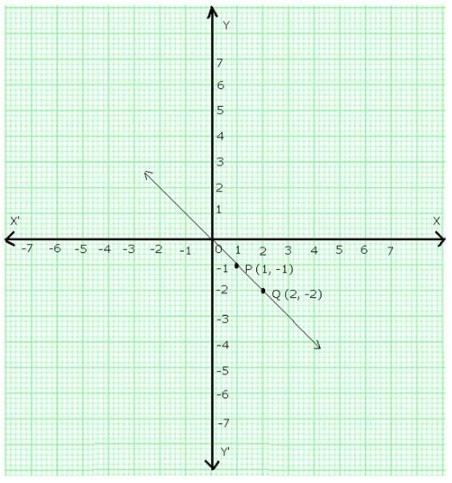
Join PQ and extend it in both the directions. Then, line PQ is the graph of the equation y = -x.