Ellipse is the locus of a point in a plane which moves in such a way that the ratio of the distance from a fixed point (focus) in the same plane to its distance from a fixed straight line (directrix) is always constant, which is always less than unity.
Major and Minor Axes
The line segment through the foci of the ellipse with its end points on the ellipse, is called its major axis.
The line segment through the centre and perpendicular to the major axis with its end points on the ellipse, is called its minor axis.
Horizontal Ellipse i.e., x2 / a2 + y2 / b2 = 1, 0 < b < a
If the coefficient of x2 has the larger denominator, then its major axis lies along the x-axis, then it is said to be horizontal ellipse.
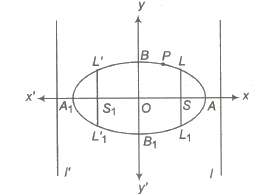
(i) Vertices A( a, 0), Al (- a, 0)
(ii) Centre (0, 0)
(iii) Major axis, AAl = 2a; Minor axis, BBl = 2b
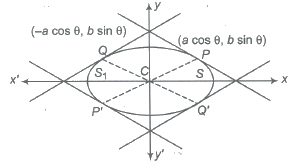
(iv) Foci are S(ae, 0) and Sl(-ae, 0)
(v) Directrices are l : x = a / e, l’ ; x = – a / e
(vi) Latusrectum, LLl = L’ Ll‘ = 2b2 / a
(vii) Eccentricity, e = √1 – b2 / a2 < 1
(viii) Focal distances are SP and SlP i.e., a – ex and a + ex. Also, SP + SlP = 2a = major axis.
(ix) Distance between foci = 2ae
(x) Distance between directrices = 2a / e
Vertical Ellipse i.e., x2 / a2 + y2 / b2 = 1, 0 < a < b
If the coefficient of x2 has the smaller denominator, then its major axis lies along the y-axis, then it is said to be vertical ellipse.
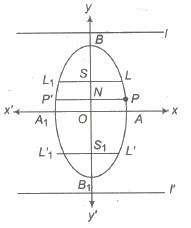
(i) Vertices B(O, b), Bl(0,- b)
(ii) Centre O(0,0)
(iii) Major axis BBl = 2b; Minor axis AAl = 2a
(iv) Foci are S(0, ae) and Sl(0, – ae)
(v) Directrices are l : y = b / e ; l’ : y = – b / e
(vi) Latusrectum LLl = L’Ll‘ = 2a2 / b
(vii) Eccentricity e = √1 – a2 / b2 < 1
(viii) Focal distances are SP and SlP.
i.e., b – ex and b + ex axis.
Also, SP + SlP = 2b = major axis.
(ix) Distance between foci = 2be
(x) Distance between directrices = 2b / e
Ordinate and Double Ordinate
Let P be any point on the ellipse and PN be perpendicular to the major axis AA’, such that PN produced meets the ellipse at P’. Then, PN is called the ordinate of P and PNP’ is the double ordinate of P .
Special Form of Ellipse
If centre of the ellipse is (h, k) and the direction of the axes are parallel to the coordinate axes, then its equation is (x – h)2 / a2 + (y – k)2 / b2 = 1
Position of a Point with Respect to an Ellipse
The point (x1, y1) lies outside, on or inside the ellipse x2 / a2 + y2 / b2 = 1 according as x21 / a2 + y21 / b2 – 1 > 0, = or < 0.
Auxiliary Circle
the ellipse x2 / a2 + y2 / b2 = 1, becomes the ellipse x2 + y2 = a2, if b = a. This is called auxiliary circle of the ellipse. i. e. , the circle described on the major axis of an ellipse as diameter is called auxiliary circle.
Director Circle
The locus of the point of intersection of perpendicular tangents to an ellipse is a director circle. If equation of an ellipse is x2 / a2 + y2 / b2 = 1, then equation of director circle is x2+ y2 = a2 + b2.
Eccentric Angle of a Point
Let P be any point on the ellipse x2 / a2 + y2 / b2 = 1. Draw PM perpendicular a b from P on the major axis of the ellipse and produce MP to the auxiliary circle in Q. Join CQ. The ∠ ACQ = φ is called the eccentric angle of the point P on the ellipse.

Parametric Equation
The equation x = a cos φ, y = b sin φ, taken together are called the parametric equations of the ellipse x2 / a2 + y2 / b2 = 1 , where φ is any parameter.
Equation of Chord
Let P(a cos θ, b sin θ) and Q(a cos φ, b sin φ) be any two points of the ellipse x2 / a2 + y2/ b2 = 1.
(i) The equation of the chord joining these points will be
(y – b sin θ) = b sin φ – b sin θ / a cos φ – a sin θ (x – a cos θ)
or x / a cos ( θ + φ / 2) + y / b sin ( θ + φ / 2) = cos ( θ – φ / 2)
(ii) The equation of the chord of contact of tangents drawn from an point (x1, y1) to the ellipse
x2 / a2 + y2 / b2 = 1 is xx1 / a2 + yy1 / b2 = 1.
(iii) The equation of the chord of the ellipse x2 / a2 + y2 / b2 = 1 bisected at the point (x1, y1) is given by
xx1 / a2 + yy1 / b2 – 1 = x21 / a2 + y21 / b2 – 1
or T = S1
Equation of Tangent
(i) Point Form The equation of the tangent to the ellipse x2 / a2 + y2 / b2 = 1 at the point (x1, y1) is xx1 / a2 + yy1 / b2 = 1.
(ii) Parametric Form The equation of the tangent to the ellipse at the point (a cos θ, b sin θ) is x / a cos θ + y / b sin θ = 1.
(iii) Slope Form The equation of the tangent of slope m to the ellipse x2 / a2 + y2 / b2 = 1 are y = mx ± √a2m2 + b2 and the coordinates of the point of contact are
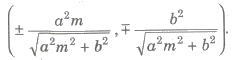
(iv) Point of Intersection of Two Tangents The equation of the tangents to the ellipse at points P(a cosθ1, b sinθ1) and Q (a cos θ2, b sinθ2) are
x / a cos θ1 + y / b sin θ1 = 1 and x / a cos θ2 + y / b sin θ2 = 1
and these two intersect at the point

Equation of Normal
(i) Point Form The equation of the normal at (x1, y1) to the ellipse x2 / a2 + y2 / b2 = 1 is
a2x / x1 + b2y / y1 = a2 – b2
(ii) Parametric Form The equation of the normal to the ellipse x2 / a2 + y2 / b2 = 1 at (a cos θ, b sin θ) is
ax sec θ – by cosec θ = a2 – b2
(iii) Slope Form The equation of the normal of slope m to the ellipse x2 / a2 + y2 / b2 = 1 are given by y = mx – m (a2 – b2) / √a2 + b2m2
and the coordinates of the point of contact are
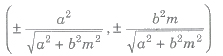
(iv) Point of Intersection of Two Normals Point of intersection of the normal at points (a cos θ1, b sin θ1) and (a cos θ2, b sin θ2) are given by
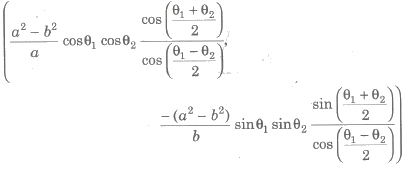
(v) If the line y = mx + c is a normal to the ellipse x2 / a2 + y2 / b2 = 1, then
c2 = m2(a2 – b2)2 / a2 + b2m2
Conormal Points
The points on the ellipse, the normals at which the ellipse passes through a given point are called conormal points.

Here, P, Q, R and S are the conormal points.
(i) The sum of the eccentric angles of the conormal points on the ellipse, x2 / a2 + y2 / b2 = 1 is an odd multiple of π.
(ii) If θ1, θ2, θ3 and θ4 are eccentric angles of four points on the ellipse, the normals at which are concurrent, then
(a) Σ cos (θ1 + θ2) = 0
(b) Σ sin (θ1 + θ2) = 0
(iii) If θ1, θ2 and θ3 are the eccentric angles of three points on the ellipse x2 / a2 + y2 / b2= 1, such that
sin (θ1 + θ2) + sin (θ2 + θ3) + sin (θ3 + θ1) = 0,
then the normal at these points are concurrent.
(iv) If the normal at four points P(x1, y1) , Q(x2, y2), R(x3, y3) and S(x4, y4) on the ellipse x2 / a2 + y2 / b2 = 1, are concurrent, then
(x1 + x2 + x3 + x4) (1 / x1 + 1 / x2 + 1 / x3 + 1 / x4) = 4
Diameter and Conjugate Diameter
The locus of the mid-point of a system of parallel chords of an ellipse is called a diameter, whose equation of diameter is
y = – (b2 / a2m) x
Two diameters of an ellipse are said to be conjugate diameters, if each bisects the chords parallel to the other.
Properties of Conjugate Diameters
(i) The eccentric angles of the ends of a pair of conjugate diameters of an ellipse differ by a right angle.
(ii) The sum of the squares of any two conjugate semi-diameters of an ellipse is constant and equal to the sum of the squares of the semi-axis of the ellipse i. e., CP2 + CD2 = a2 + b2.
(iii) If CP, CQ are two conjugate semi-diameters of an ellipse x2 / a2 + y2 / b2 = 1 and S, S1 be two foci of an ellipse, then
SP * S1P = CQ2
(iv) The tangent at the ends of a pair of conjugate diameters of an ellipse form a parallelogram.
(v) The area of the parallelogram formed by the tangents at the ends of conjugate diameters of an ellipse is constant and is equal to the product of the axis.
Important Points
1. The point P(x1 y1) lies outside, on or inside the ellipse x2 / a2 + y2 / b2 = 1 according as x21 / a2 + y21 / b2 – 1 > 0, or < 0.
2. The line y = mx + c touches the ellipse
x2 / a2 + y2 / b2 = 1, if c2 = a2m2 + b2
3. The combined equation of the pair of tangents drawn from a point (x1 y1) to the ellipse x2 / a2 + y2 / b2 = 1 is
(x2 / a2 + y2 / b2 – 1) (x21 / a2 + y21 / b2 – 1) = (xx1 / a2 + yy1 / b2 – 1)2
i.e, SS1 = T2
4. The tangent and normal at any point of an ellipse bisect the external and internal angles between the focal radii to the point.
5. If SM and S’ M’ are perpendiculars from the foci upon the tangent at any point of the ellipse, then SM x S’ M’ = b2 and M, M’ lie on the auxiliary circle.
6. If the tangent at any point P on the ellipse x2 / a2 + y2 / b2 = 1 meets the major axis in T and minor axis in T’, then CN * CT = a2 ,CN’ * Ct’ = p2, where N and N’ are the foot of the perpendiculars from P on the respective axis.
7. The common chords of an ellipse and a circle are equally inclined to the axes of the ellipse.
8. The four normals can be drawn from a point on an ellipse.
9. Polar of the point (x1 y1) with respect to the ellipse x2 / a2 + y2 / b2 = 1 is xx1 / a2 + yy1/ b2 = 1.
Here, point (x1 y1) is the pole of xx1 / a2 + yy1 / b2 = 1.
10. The pole of the line lx + my + n = 0 with respect to ellipse x2 / a2 + y2 / b2 = 1 is
p(-a2l / n, -b2m / n).
11. Two tangents can be drawn from a point P to an ellipse. These tangents are real and distinct or coincident or imaginary according as the given point lies outside, on or inside the ellipse.
12. Tangents at the extremities of latusrectum of an ellipse intersect on the corresponding direction.
13. Locus of mid-point of focal chords of an ellipse x2 / a2 + y2 / b2 = 1 is
x2 / a2 + y2 / b2 = ex / a2.
14. Point of intersection of the tangents at two points on the ellipse x2 / a2 + y2 / b2 = 1, whose eccentric angles differ by a right angles lies on the ellipse x2 / a2 + y2 / b2 = 2.
15. Locus of mid – point of normal chords of an ellipse x2 / a2 + y2 / b2 = 1 is
(x2 / a2 + y2 / b2)2 (a6 / x2 + b6 / y2) = (a2 – b2)2.
16. Eccentric angles of the extremities of latusrectum of an ellipse x2 / a2 + y2 / b2 = 1 are
tan-1 ( ± b / ae).
17. The straight lines y = m1x and y =m2x are conjugate diameters of an ellipse x2 / a2 + y2 / b2 = 1, if m1m2 = – b2 / a2.
18. The normal at point P on an ellipse with foci S, S1 is the internal bisector of ∠ SPS1.