Conic Section
A conic is the locus of a point whose distance from a fixed point bears a constant ratio to its distance from a fixed line. The fixed point is the focus S and the fixed line is directrix l.
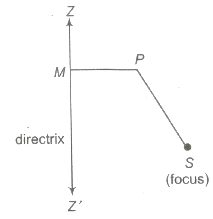
The constant ratio is called the eccentricity denoted by e.
- If 0 < e < 1, conic is an ellipse.
- e = 1, conic is a parabola.
- e > 1, conic is a hyperbola.
- If fixed point of curve is (x1, y1) and fixed line is ax + by + c = then equation of the conic is
(a2 + b2) [(x — x1)2 + (y — y1)2] = e2(ax + by + c)2
General Equation of Conic
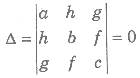
A second degree equation ax2 + 2hxy + by2 + 2gx + 2fy + c= 0 represents
- Pair of straight lines, if
- Circle, if a = b, h = 0
- Parabola, if h2 = ab and Δ ≠ 0
- Ellipse, if h2 < ab and Δ ≠ 0
- Hyperbola, if h2 > ab and Δ ≠ 0
- Rectangular hyperbola, if a + b = 0 and Δ ≠ 0
Parabola
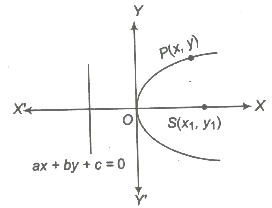
A parabola is the locus of a point which moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from a fixed straight line in the same plane.
If focus of a parabola is S(x1, y1) and equation of the directrix is ax + by + c = 0, then the equation of the parabola is
(a2 + b2)[(x – x1)2 + (y – y1)2] = (ax + by + c)2
Definitions Related to Parabola
- Vertex The intersection point of parabola and axis.
- Centre The point which bisects every chord of the conic passing through it.
- Focal Chord Any chord passing through the focus.
- Double Ordinate A chord perpendicular to the axis of a conic.
- Latusrectum A double ordinate passing through the focus of the parabola.
- Focal Distance The distance of a point P(x, y) from the focus S is called the focal distance of the point P.

Other Forms of a Parabola
If the vertex of the parabola is at a point A(h , k) and its latusrectum is of length 4a, then its equation is
- (y – k)2 = 4a (x – h), its axis is parallel to OX i. e. , parabola open rightward.
- (y – k)2 = – 4a (x – h), its axis is parallel to OX’ i. e., parabola open leftward.
- (x – h)2 = – 4a (y – k), its axis is parallel to OY i.e., parabola open upward.
- (x – h)2 = – 4a (y – k), its axis is parallel to OY ‘ i.e., parabola open downward. –
- The general equation of a parabola whose axis is parallel to X – axis is x = ay2 + by + c and the general equation of a parabola whose axis is parallel to Y-axis is y = ax2 + bx + c.
Position of a Point
The point (x1, y1) lies outside, on or inside the parabola y2 = 4ax according as y12 — 4ax1>, =, < 0.
Chord
Joining any two points on a curve is called chord.
(i) Parametric Equation of a Chord Let P(at12 , 2at1) and Q (at22, 2at2) be any two points on the parabola y1 = 4ax, then the equation of the chord is
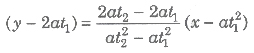
or y (t1 + t1) = 2x + 2at1t2
(ii) Let P(at2 , 2at) be the one end of a focal chord PQ of the parabola y2 = 4ax, then the coordinates of the other end Q are
(a/t2, -2a/t)
(iii) If l1 and l2 are the length of the focal segments, then length of the latusrectum = 2 (harmonic mean of focal segment)
i.e., 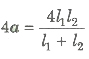
(iv) For a chord joining points P(at12 , 2at1) and Q(at22 , 2at2) and passing through focus, then t1t2 = 1.
(v) Length of the focal chord having t1 and t2 as end points is a (t1 — t1)2.
(vi) Chord of contact drawn from a point (x1, y1) to the parabola y2 = 4ax is yy1, = 2a (x + x1)
(vii) Equation of the chord of the parabola y2 = 4ax, which is bisected at (x1 , y1) is given by
T = S1
i.e. , yy1 — 2a (x + x1) = y12 – 4ax
Equation of Tangent
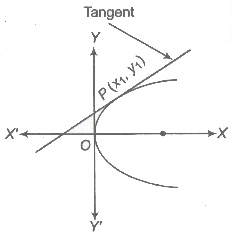
A line which touch only one point of a parabola.
(i) Point Form The equation of the tangent to the parabola y2 = 4ax at a point (x1, y1) is given by yy1 = 2a (x + x1)
(ii) Slope Form
(a) The equation of the tangent of slope m to the parabola y2 = 4ax is
y = (mx + a/m)
(b) The equation of the tangent of slope m to the parabola (y – k)2 = 4a (x – h) is given by
(y – k)2 = m (x — h) + a/m
The coordinates of the point of contact are

(iii) Parametric Form The equation of the tangent to the parabola y2 = 4ax at a point (at2, 2at) is yt = x + at2
(iv) The line y = mx + c touches a parabola, if c = a/m and the point of contact is
(v) Point of Intersection of Two Tangents Let two tangents at P(at12 , 2at1) and Q(at22, 2at2) intersect at R. Then, their point of intersection is R[at1t2, a(t1 + t2)] i.e., (GM of abscissa, AM of ordinate).
(vi) The straight line lx + my + n = 0 touches y2 = 4ax, if nl = am2 and x cos α + y sin α = p touches y2 = 4ax, if p cos α + a sin2 α = 0.
(vii) Angle θ between tangents at two points P(at1t2 , 2at1) and Q(at22, 2at2) on the parabola y2 = 4ax is given by

(viii) The combined equation of the pair of tangents drawn from a point to a parabola y2 = 4ax is given by
SS1 = T2
where, S = y2 – 4ax, S1= y12 – 4ax1
and T = [yy1 – 2a (x + x1)]
Important Results on Tangents
- The tangent at any point on a parabola bisects the angle between the focal distance of the point and the perpendicular on the directrix from the point.
- The tangent at the extremities of a focal chord of a parabola intersect at right angle on the directrix.
- The portion of the tangent to a parabola cut off between the directrix and the curve subtends a right angle at the focus.
- The perpendicular drawn from the focus on any tangent to a parabola intersect it at the point where it cuts the tangent at the vertex.
- The orthocentre of any triangle formed by three tangents to a parabola lies on the directrix.
- The circumcircle formed by the intersection points of tangents at any three points on a parabola passes through the focus of the parabola.
- The tangent at any point of a parabola is equally inclined to the focal distance of the point and the axis of the parabola.
- The length of the subtangent at any point on a parabola is equal to twice the abscissa of the point.
- Two tangents can be drawn from a point to a parabola. Two tangents are real and distinct or coincident or imaginary according as given point lies outside, on or inside the parabola.
Equation of Normal
A line which is perpendicular to the tangent.
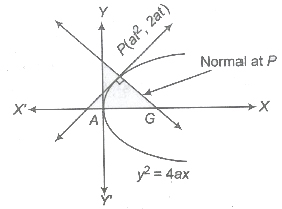
- Point Form The equation of the normal to the parabola y2 = 4ax at a point (x1, y1) is given by y – y1 = -y1/2a(x — x1).
- Parametric Form The equation of the normal to the parabola y2 = 4ax at point (at2, 2at) is given by y + tx = 2at + at3
- Slope Form The equation of the normal to the parabola y2 = 4ax in terms of its slope m is given by y = mx — 2am — am3 at point (am2, — 2am).
Important Results on Normals
- If the normal at the point P(at12,2at1) meets the parabola y2 = 4ax at Q(a22,2at2), then t2 = -t – 2/t1.
- The tangent at one extremity of the focal chord of a parabola is parallel to the normal at other extremity.
- The normal at points P(at12,2at1) and Q(a22,2at2) to the parabola y2 = 4ax intersect at the point
[2a + a(t12 + t22+ t1t2)], – at1t2(t1 + t2). - If the normal at points P(at12,2at1) and Q(a22,2at2) on the parabola y2 = 4ax meet on the parabola, then t1t2 = 2.
- If the normal at two points P and Q of a parabola y2 = 4ax intersect at a third point R on the curve, then the product of the ordinates of P and Q is 8a2.
- If the normal chord at a point P(at2 ,2at)to the parabola y2 = 4ax subtends a right angle at the vertex of the parabola, then t2 = 2.
- The normal chord of a parabola at a point whose ordinate is equal to the abscissa, subtends a right angle at the focus.
- The normal at any point of a parabola is equally inclined to the focal distance of the point and the axis of the parabola.
- Three normals can be drawn from a point to a parabola.
- Conormai The points on the parabola at which the normals pass through a common point are called conormal points. The conormal points are called the feet of the normals.
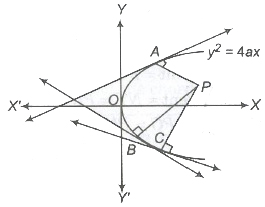
Points A, B and Care called conormal points.
- The algebraic sum of the slopes of the normals at conormals point is O.
- The sum of the ordinates of the conormal points is O.
- The centroid of the triangle formed by the conormal points on a parabola lies on its axis.
Director Circle
- The locus of the point of intersection of perpendicular tangents to a conic is known as director circle.
- The director circle of a parabola is its directrix.
Equation of Diameter
- The locus of mid-point of a system of parallel chords of a conic is known its diameter.
- The diameter bisecting chords of slope m to the parabola y2 = 4ax is y = 2a/m
Length of Tangent and Normal
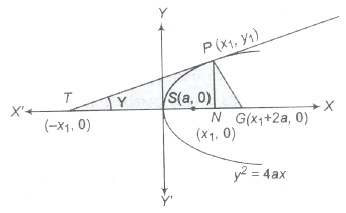
- The length of the tangent = PT = PN cosec Ψ = y1 cosec Ψ
- The length of subtangent = NT = PN cot Ψ = y1 cot Ψ
- The length of normal = PG = PN sec Ψ = y1 sec Ψ
- The length of subnormal = NG = PN tan Ψ = y1 tan Ψ
Pole and Polar
Let P be a point lying within or outside a given parabola. Suppose any straight line drawn through P intersects the parabola at Q and R. Then, the locus of the point of intersection of the tangents to the parabola at Q and R is called the polar of the given point P with respect to the parabola and the point P is called the pole of the polar.
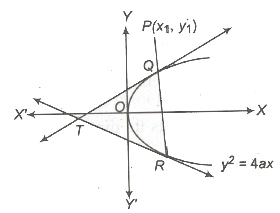
- The polar of a point P(x1, 1) with respect to the parabola y2 = 4ax is yy1 = 2a(x + x1) or T = 0.
- Any tangent is the polar of its point of contact.
- Pole of lx + my + n = 0 with respect to y2 = 4ax is

- Pole of the chord joining (x1, y1) and (x1, y1) is

- If the polar of P(x1, y1)passes through Q(x2 ,y2), then the polar of Q will passes through P. Here, P and Q are called conjugate points.
- If the pole of a line a1x + b1y + c1 = 0 lies on another line a2x + b2y + c2 = 0, then the pole of the second line will lies on the first line. Such lines are called conjugate lines.
- The point of intersection of the polar of two points Q and R is the pole of QR.
- The tangents at the ends of any chord of the parabola meet on the diameter which bisect the chord.
Important Points to be Remembered
(i) For the ends of latusrectum of the parabola y2 = 4ax, the values of the perimeter are ± 1.
(ii) The circles described on focal radii of a parabola as diameter touches the tangent at the vertex.
(iii) The straight line y =mx + c meets the parabola y2 = 4ax in two points. These two points are real and distinct, if c > a/m, points are real and coincident, if c = a/m, points are imaginary, if c < a/m.
(iv) Area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.
(v) The circles described on any focal chord of a parabola as diameter touches the directrix.
(vi) If y1, y2, y3 are the ordinates of the vertices of a triangle inscribed in the parabola y2 = 4ax, then its area is 1/8a (y1 – y2) (y2 – y3) (y3 – y1).