Chapter 6 Lines and Angles RS Aggarwal Solution for Class 9th Maths

Angles, Linesand Triangles

Question 1:

Exercise 4A

1. Angle: Two rays having a common end point form an angle.
2. Interior of an angle: The interior of ∠AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
3. Obtuse angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.
4. Reflex angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle.
5. Complementary angles: Two angles are said to be complementary, if the sum of their measures is 90o.
6. Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°.

Question 2:

∠A = 36° 27′ 46″ and ∠B = 28° 43′ 39″

∴ Their sum = (36° 27′ 46″) + (28° 43′ 39″)

Therefore, the sum ∠A + ∠B = 65° 11′ 25″

Question 3:

Let ∠A = 36° and ∠B = 24° 28′ 30″ Their difference = 36° – 24° 28′ 30″

Thus the difference between two angles is ∠A – ∠B = 11° 31′ 30″

Question 4:

• 1. Complement of 58o = 90o – 58o = 32o
  2. Complement of 16o = 90 – 16o = 74o
  3. 
     of a right angle =
     
     × 90o = 60o Complement of 60o = 90o – 60o = 30o
  4. 1o = 60′

⇒ 90o = 89o 60′

Complement of 46o 30′ = 90o – 46o 30′ = 43o 30′ (v) 90o = 89o 59′ 60″

Complement of 52o 43′ 20″ = 90o – 52o 43′ 20″

= 37o 16′ 40″

(vi) 90o = 89o 59′ 60″

∴ Complement of (68o 35′ 45″)

= 90o – (68o 35′ 45″)

= 89o 59′ 60″ – (68o 35′ 45″)

= 21o 24′ 15″

Question 5:

1. Supplement of 63o = 180o – 63o = 117o
2. Supplement of 138o = 180o – 138o = 42o
3. 
   of a right angle =
   
   × 90o = 54o

∴ Supplement of 54o = 180o – 54o = 126o

1. 1o = 60′

⇒ 180o = 179o 60′

Supplement of 75o 36′ = 180o – 75o 36′ = 104o 24′ (v) 1o = 60′, 1′ = 60″

⇒ 180o = 179o 59′ 60″

Supplement of 124o 20′ 40″ = 180o – 124o 20′ 40″

= 55o 39′ 20″

(vi) 1o = 60′, 1′ = 60″

⇒ 180o = 179o 59′ 60″

∴ Supplement of 108o 48′ 32″ = 180o – 108o 48′ 32″

= 71o 11′ 28″.

Question 6:

• 1. 
     Let the required angle be xo Then, its complement = 90o – xo

∴ The measure of an angle which is equal to its complement is 45o.

• 1. 
     Let the required angle be xo Then, its supplement = 180o – xo

∴ The measure of an angle which is equal to its supplement is 90o.

Question 7:

Let the required angle be xo Then its complement is 90o – xo

∴ The measure of an angle which is 36o more than its complement is 63o.

Question 8:

Let the required angle be xo Then its supplement is 180o – xo

∴ The measure of an angle which is 25o less than its supplement is

Question 9:

Let the required angle be xo Then, its complement = 90o – xo

∴ The required angle is 72o.

Question 10:

Let the required angle be xo Then, its supplement is 180o – xo

∴ The required angle is 150o.

Question 11:

Let the required angle be xo

Then, its complement is 90o – xo and its supplement is 180o – xo That is we have,

∴ The required angle is 60o.

Question 12:

Let the required angle be xo

Then, its complement is 90o – xo and its supplement is 180o – xo

∴ The required angle is 45o.

Question 13:

Let the two required angles be xo and 180o – xo. Then,

⇒ 2x = 3(180 – x)

⇒ 2x = 540 – 3x

⇒ 3x + 2x = 540

⇒ 5x = 540

⇒ x = 108

Thus, the required angles are 108o and 180o – xo = 180 o – 108o = 72o.

Question 14:

Let the two required angles be xo and 90o – xo. Then

⇒ 5x = 4(90 – x)

⇒ 5x = 360 – 4x

⇒ 5x + 4x = 360

⇒ 9x = 360

⇒ x =

= 40

Thus, the required angles are 40o and 90o – xo = 90 o – 40o = 50o.

Question 15:

Let the required angle be xo.

Then, its complementary and supplementary angles are (90o – x) and (180o – x) respectively.

Then, 7(90o – x) = 3 (180o – x) – 10o

⇒ 630o – 7x = 540o – 3x – 10o

⇒ 7x – 3x = 630o – 530o

⇒ 4x = 100o

⇒ x = 25o

Thus, the required angle is 25o.

Question 1:

Exercise 4B

Since ∠BOC and ∠COA form a linear pair of angles, we have

∠BOC + ∠COA = 180o

⇒ xo + 62o = 180o

⇒ x = 180 – 62

∴ x = 118o

Question 2:

Since, ∠BOD and ∠DOA form a linear pair.

∠BOD + ∠DOA = 180o

∴ ∠BOD + ∠DOC + ∠COA = 180o

⇒ (x + 20)o + 55o + (3x – 5)o = 180o

⇒ x + 20 + 55 + 3x – 5 = 180

⇒ 4x + 70 = 180

⇒ 4x = 180 – 70 = 110

⇒ x =

= 27.5

∴ ∠AOC = (3 × 27.5 – 5)o = 82.5-5 = 77.5o And, ∠BOD = (x + 20)o = 27.5o + 20o = 47.5o.

Question 3:

Since ∠BOD and ∠DOA from a linear pair of angles.

⇒ ∠BOD + ∠DOA = 180o

⇒ ∠BOD + ∠DOC + ∠COA = 180o

⇒ xo + (2x – 19)o + (3x + 7)o = 180o

⇒ 6x – 12 = 180

⇒ 6x = 180 + 12 = 192

⇒ x =

= 32

⇒ x = 32

⇒ ∠AOC = (3x + 7)o = (3 32 + 7)o = 103o

⇒ ∠COD = (2x – 19)o = (2 32 – 19)o = 45o

and ∠BOD = xo = 32o

Question 4:

x: y: z = 5: 4: 6

The sum of their ratios = 5 + 4 + 6 = 15 But x + y + z = 180o

[Since, XOY is a straight line]

So, if the total sum of the measures is 15, then the measure of x is 5. If the sum of angles is 180o, then, measure of x =

× 180 = 60

And, if the total sum of the measures is 15, then the measure of y is 4. If the sum of the angles is 180o, then, measure of y =

× 180 = 48 And ∠z = 180o – ∠x – ∠y

= 180o – 60o – 48o

= 180o – 108o = 72o

∴ x = 60, y = 48 and z = 72.

Question 5:

AOB will be a straight line, if two adjacent angles form a linear pair.

∴ ∠BOC + ∠AOC = 180o

⇒ (4x – 36)o + (3x + 20)o = 180o

⇒ 4x – 36 + 3x + 20 = 180

⇒ 7x – 16 = 180o

⇒ 7x = 180 + 16 = 196

⇒ x =

= 28

∴ The value of x = 28.

Question 6:

Since ∠AOC and ∠AOD form a linear pair.

∴ ∠AOC + ∠AOD = 180o

⇒ 50o + ∠AOD = 180o

⇒ ∠AOD = 180o – 50o = 130o

∠AOD and ∠BOC are vertically opposite angles.

∠AOD = ∠BOC

⇒ ∠BOC = 130o

∠BOD and ∠AOC are vertically opposite angles.

∴ ∠BOD = ∠AOC

⇒ ∠BOD = 50o

Question 7:

Since ∠COE and ∠DOF are vertically opposite angles, we have,

∠COE = ∠DOF

⇒ ∠z = 50o

Also ∠BOD and ∠COA are vertically opposite angles. So, ∠BOD = ∠COA

⇒ ∠t = 90o

As ∠COA and ∠AOD form a linear pair,

∠COA + ∠AOD = 180o

⇒ ∠COA + ∠AOF + ∠FOD = 180o [∠t = 90o]

⇒ t + x + 50o = 180o

⇒ 90o + xo + 50o = 180o

⇒ x + 140 = 180

⇒ x = 180 – 140 = 40

Since ∠EOB and ∠AOF are vertically opposite angles So, ∠EOB = ∠AOF

⇒ y = x = 40

Thus, x = 40 = y = 40, z = 50 and t = 90

Question 8:

Since ∠COE and ∠EOD form a linear pair of angles.

⇒ ∠COE + ∠EOD = 180o

⇒ ∠COE + ∠EOA + ∠AOD = 180o

⇒ 5x + ∠EOA + 2x = 180

⇒ 5x + ∠BOF + 2x = 180

[∴ ∠EOA and BOF are vertically opposite angles so, ∠EOA = ∠BOF]

⇒ 5x + 3x + 2x = 180

⇒ 10x = 180

⇒ x = 18

Now ∠AOD = 2xo = 2 × 18o = 36o

∠COE = 5xo = 5 × 18o = 90o

and, ∠EOA = ∠BOF = 3xo = 3 × 18o = 54o

Question 9:

Let the two adjacent angles be 5x and 4x. Now, since these angles form a linear pair. So, 5x + 4x = 180o

⇒ 9x = 180o

⇒ x =

= 20

∴ The required angles are 5x = 5x = 5 20o = 100o and 4x = 4 × 20o = 80o

Question 10:

Let two straight lines AB and CD intersect at O and let ∠AOC = 90o.

Now, ∠AOC = ∠BOD [Vertically opposite angles]

⇒ ∠BOD = 90o

Also, as ∠AOC and ∠AOD form a linear pair.

⇒ 90o + ∠AOD = 180o

⇒ ∠AOD = 180o – 90o = 90o

Since, ∠BOC = ∠AOD [Verticallty opposite angles]

⇒ ∠BOC = 90o

Thus, each of the remaining angles is 90o.

Question 11:

Since, ∠AOD and ∠BOC are vertically opposite angles.

∴ ∠AOD = ∠BOC

Now, ∠AOD + ∠BOC = 280o [Given]

⇒ ∠AOD + ∠AOD = 280o

⇒ 2∠AOD = 280o

⇒ ∠AOD =

= 140o

⇒ ∠BOC = ∠AOD = 140o

As, ∠AOC and ∠AOD form a linear pair. So, ∠AOC + ∠AOD = 180o

⇒ ∠AOC + 140o = 180o

⇒ ∠AOC = 180o – 140o = 40o

Since, ∠AOC and ∠BOD are vertically opposite angles.

∴ ∠AOC = ∠BOD

⇒ ∠BOD = 40o

∴ ∠BOC = 140o, ∠AOC = 40o , ∠AOD = 140o and ∠BOD = 40o.

Question 12:

Since ∠COB and ∠BOD form a linear pair So, ∠COB + ∠BOD = 180o

⇒ ∠BOD = 180o – ∠COB …. (1)

Also, as ∠COA and ∠AOD form a linear pair. So, ∠COA + ∠AOD = 180o

⇒ ∠AOD = 180o – ∠COA

⇒ ∠AOD = 180o – ∠COB …. (2)

[Since, OC is the bisector of ∠AOB, ∠BOC = ∠AOC] From (1) and (2), we get,

∠AOD = ∠BOD (Proved)

Question 13:

Let QS be a perpendicular to AB. Now, ∠PQS = ∠SQR

Because angle of incident = angle of reflection

⇒ ∠PQS = ∠SQR =

= 56o

Since QS is perpendicular to AB, ∠PQA and ∠PQS are complementary angles. Thus, ∠PQA + ∠PQS = 90o

⇒ ∠PQA + 56o = 90o

⇒ ∠PQA = 90o – 56o = 34o

Question 14:

Given : AB and CD are two lines which are intersecting at O. OE is a ray bisecting the

∠BOD. OF is a ray opposite to ray OE.

To Prove: ∠AOF = ∠COF

Proof : Since

and

are two opposite rays,

is a straight line passing through O.

∴ ∠AOF = ∠BOE and ∠COF = ∠DOE

[Vertically opposite angles] But ∠BOE = ∠DOE (Given)

∴ ∠AOF = ∠COF

Hence, proved.

Question 15:

Given:

is the bisector of ∠BCD and

is the bisector of ∠ACD. To Prove: ∠ECF = 90o

Proof: Since ∠ACD and ∠BCD forms a linear pair.

∠ACD + ∠BCD = 180o

∠ACE + ∠ECD + ∠DCF + ∠FCB = 180o

∠ECD + ∠ECD + ∠DCF + ∠DCF = 180o

because ∠ACE = ∠ECD and ∠DCF = ∠FCB

2(∠ECD) + 2 (∠CDF) = 180o

2(∠ECD + ∠DCF) = 180o

∠ECD + ∠DCF =

= 90o

∠ECF = 90o (Proved)

Question 1:

Exercise 4C

Since AB and CD are given to be parallel lines and t is a transversal. So, ∠5 = ∠1 = 70o [Corresponding angles are equal]

∠3 = ∠1 = 70o [Vertically opp. Angles]

∠3 + ∠6 = 180o [Co-interior angles on same side]

∴ ∠6 = 180o – ∠3

= 180o – 70o = 110o

∠6 = ∠8 [Vertically opp. Angles]

⇒ ∠8 = 110o

⇒ ∠4 + ∠5 = 180o [Co-interior angles on same side]

∠4 = 180o – 70o = 110o

∠2 = ∠4 = 110o [ Vertically opposite angles]

∠5 = ∠7 [Vertically opposite angles] So, ∠7 = 70o

∴ ∠2 = 110o, ∠3 = 70o , ∠4 = 110o, ∠5 = 70o, ∠6 = 110o, ∠7 = 70o and ∠8 = 110o.

Question 2:

Since ∠2 : ∠1 = 5 : 4.

Let ∠2 and ∠1 be 5x and 4x respectively.

Now, ∠2 + ∠1 = 180o , because ∠2 and ∠1 form a linear pair. So, 5x + 4x = 180o

⇒ 9x = 180o

⇒ x = 20o

∴ ∠1 = 4x = 4 × 20o = 80o And ∠2 = 5x = 5 × 20o = 100o

∠3 = ∠1 = 80o [Vertically opposite angles]

And ∠4 = ∠2 = 100o [Vertically opposite angles]

∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles] So, ∠5 = 80o and ∠6 = 100o

∠8 = ∠6 = 100o [Vertically opposite angles] And ∠7 = ∠5 = 80o [Vertically opposite angles]

Thus, ∠1 = 80o, ∠2 = 100o, ∠3 = ∠80o, ∠4 = 100o, ∠5 = 80o, ∠6 = 100o, ∠7 = 80o and

∠8 = 100o.

Question 3:

Given: AB || CD and AD || BC To Prove: ∠ADC = ∠ABC

Proof: Since AB || CD and AD is a transversal. So sum of consecutive interior angles is

180o.

⇒ ∠BAD + ∠ADC = 180o ….(i)

Also, AD || BC and AB is transversal. So, ∠BAD + ∠ABC = 180o ….(ii) From (i) and (ii) we get:

∠BAD + ∠ADC = ∠BAD + ∠ABC

⇒ ∠ADC = ∠ABC (Proved)

Question 4:

1. 
   Through E draw EG || CD. Now since EG||CD and ED is a transversal.

So, ∠GED = ∠EDC = 65o [Alternate interior angles] Since EG || CD and AB || CD,

EG||AB and EB is transversal.

So, ∠BEG = ∠ABE = 35o [Alternate interior angles] So, ∠DEB = xo

⇒ ∠BEG + ∠GED = 35o + 65o = 100o.

Hence, x = 100.

1. 
   Through O draw OF||CD.

Now since OF || CD and OD is transversal.

∠CDO + ∠FOD = 180o

[sum of consecutive interior angles is 180o]

⇒ 25o + ∠FOD = 180o

⇒ ∠FOD = 180o – 25o = 155o

As OF || CD and AB || CD [Given] Thus, OF || AB and OB is a transversal.

So, ∠ABO + ∠FOB = 180o [sum of consecutive interior angles is 180o]

⇒ 55o + ∠FOB = 180o

⇒ ∠FOB = 180o – 55o = 125o

Now, xo = ∠FOB + ∠FOD = 125o + 155o = 280o.

Hence, x = 280.

1. 
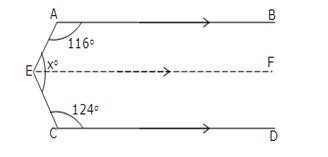
   Through E, draw EF || CD.

Now since EF || CD and EC is transversal.

∠FEC + ∠ECD = 180o

[sum of consecutive interior angles is 180o]

⇒ ∠FEC + 124o = 180o

⇒ ∠FEC = 180o – 124o = 56o

Since EF || CD and AB ||CD

So, EF || AB and AE is a trasveral.

So, ∠BAE + ∠FEA = 180o

[sum of consecutive interior angles is 180o]

∴ 116o + ∠FEA = 180o

⇒ ∠FEA = 180o – 116o = 64o

Thus, xo = ∠FEA + ∠FEC

= 64o + 56o = 120o.

Hence, x = 120.

Question 5:

Since AB || CD and BC is a transversal.

So, ∠ABC = ∠BCD [atternate interior angles]

⇒ 70o = xo + ∠ECD ….(i)

Now, CD || EF and CE is transversal.

So, ∠ECD + ∠CEF = 180o

∴ ∠ECD + 130o = 180o

[sum of consecutive interior angles is 180o]

⇒ ∠ECD = 180o – 130o = 50o

Putting ∠ECD = 50o in (i) we get, 70o = xo + 50o

⇒ x = 70 – 50 = 20

Question 6:

Through C draw FG || AE

Now, since CG || BE and CE is a transversal.

So, ∠GCE = ∠CEA = 20o

∴ ∠DCG = 130o – ∠GCE

= 130o – 20o = 110o

[Alternate angles]

Also, we have AB || CD and FG is a transversal.

So, ∠BFC = ∠DCG = 110o

As, FG || AE, AF is a transversal.

[Corresponding angles]

∠BFG = ∠FAE [Corresponding angles]

∴ xo = ∠FAE = 110o. Hence, x = 110

Question 7:

Given: AB || CD

To Prove: ∠BAE – ∠DCE = ∠AEC

Construction : Through E draw EF || AB Proof : Since EF || AB, AE is a transversal. So, ∠BAE + ∠AEF = 180O ….(i)

[sum of consecutive interior angles is 180o] As EF || AB and AB || CD [Given]

So, EF || CD and EC is a transversal.

So, ∠FEC + ∠DCE = 180o ….(ii)

[sum of consecutive interior angles is 180o] From (i) and (ii) we get,

∠BAE + ∠AEF = ∠FEC + ∠DCE

⇒ ∠BAE – ∠DCE = ∠FEC – ∠AEF = ∠AEC [Proved]

Question 8:

Since AB || CD and BC is a transversal.

So, ∠BCD = ∠ABC = xo

[Alternate angles]

As BC || ED and CD is a transversal.

∠BCD + ∠EDC = 180o

⇒ ∠BCD + 75o =180o

⇒ ∠BCD = 180o – 75o = 105o

∠ABC = 105o

∴ xo = ∠ABC = 105o Hence, x = 105.

[since ∠BCD = ∠ABC]

Question 9:

Through F, draw KH || AB || CD

Now, KF || CD and FG is a transversal.

⇒ ∠KFG = ∠FGD = ro …. (i) [alternate angles]

Again AE || KF, and EF is a transversal.

So, ∠AEF + ∠KFE = 180o

∠KFE = 180o – po …. (ii) Adding (i) and (ii) we get,

∠KFG + ∠KFE = 180 – p + r

⇒ ∠EFG = 180 – p + r

⇒ q = 180 – p + r i.e., p + q – r = 180

Question 10:

Since AB || PQ and EF is a transversal.

So, ∠CEB = ∠EFQ [Corresponding angles]

⇒ ∠EFQ = 75o

⇒ ∠EFG + ∠GFQ = 75o

⇒ 25o + yo = 75o

⇒ y = 75 – 25 = 50

Also, ∠BEF + ∠EFQ = 180o

∠BEF = 180o – ∠EFQ

= 180o – 75o

∠BEF = 105o

[sum of consecutive interior angles is 180o]

∴ ∠FEG + ∠GEB = ∠BEF = 105o

⇒ ∠FEG = 105o – ∠GEB = 105o – 20o = 85o

In ∆EFG we have,

xo + 25o + ∠FEG = 180o

Hence, x = 70.

Question 11:

Since AB || CD and AC is a transversal.

So, ∠BAC + ∠ACD = 180o

⇒ ∠ACD = 180o – ∠BAC

= 180o – 75o = 105o

[sum of consecutive interior angles is 180o]

⇒ ∠ECF = ∠ACD [Vertically opposite angles]

∠ECF = 105o

Now in ∆CEF,

∠ECF + ∠CEF + ∠EFC =180o

⇒ 105o + xo + 30o = 180o

⇒ x = 180 – 30 – 105 = 45

Hence, x = 45.

Question 12:

Since AB || CD and PQ a transversal.

So, ∠PEF = ∠EGH [Corresponding angles]

⇒ ∠EGH = 85o

∠EGH and ∠QGH form a linear pair. So, ∠EGH + ∠QGH = 180o

⇒ ∠QGH = 180o – 85o = 95o

Similarly, ∠GHQ + 115o = 180o

⇒ ∠GHQ = 180o – 115o = 65o

In ∆GHQ, we have, xo + 65o + 95o = 180o

⇒ x = 180 – 65 – 95 = 180 – 160

∴ x = 20

Question 13:

Since AB || CD and BC is a transversal. So, ∠ABC = ∠BCD

⇒ x = 35

Also, AB || CD and AD is a transversal. So, ∠BAD = ∠ADC

⇒ z = 75

In ∆ABO, we have,

∠AOB + ∠BAO + ∠BOA = 180o

⇒ xo + 75o + yo = 180o

⇒ 35 + 75 + y = 180

⇒ y = 180 – 110 = 70

∴ x = 35, y = 70 and z = 75.

Question 14:

Since AB || CD and PQ is a transversal. So, y = 75 [Alternate angle]

Since PQ is a transversal and AB || CD, so x + APQ = 180o

[Sum of consecutive interior angles]

⇒ xo = 180o – APQ

⇒ x = 180 – 75 = 105

Also, AB || CD and PR is a transversal.

So, ∠APR = ∠PRD [Alternate angle]

⇒ ∠APQ + ∠QPR = ∠PRD [Since ∠APR = ∠APQ + ∠QPR]

⇒ 75o + zo = 125o

⇒ z = 125 – 75 = 50

∴ x = 105, y = 75 and z = 50.

Question 15:

∠PRQ = xo = 60o

[vertically opposite angles]

Since EF || GH, and RQ is a transversal. So, ∠x = ∠y [Alternate angles]

⇒ y = 60

AB || CD and PR is a transversal.

So, ∠PRD = ∠APR [Alternate angles]

⇒ ∠PRQ + ∠QRD = ∠APR [since ∠PRD = ∠PRQ + ∠QRD]

⇒ x + ∠QRD = 110o

⇒ ∠QRD = 110o – 60o = 50o

In ∆QRS, we have,

∠QRD + to + yo = 180o

⇒ 50 + t + 60 = 180

⇒ t = 180 – 110 = 70

Since, AB || CD and GH is a transversal So, zo = to = 70o [Alternate angles]

∴ x = 60 , y = 60, z = 70 and t = 70

Question 16:

1. Lines l and m will be parallel if 3x – 20 = 2x + 10

[Since, if corresponding angles are equal, lines are parallel]

⇒ 3x – 2x = 10 + 20

⇒ x = 30

1. Lines will be parallel if (3x + 5)o + 4xo = 180o

[if sum of pairs of consecutive interior angles is 180o, the lines are parallel] So, (3x + 5) + 4x = 180

⇒ 3x + 5 + 4x = 180

⇒ 7x = 180 – 5 = 175

⇒ x =

= 25

Question 17:

Given: Two lines m and n are perpendicular to a given line l.

To Prove: m || n Proof : Since m ⊥ l So, ∠1 = 90o Again, since n ⊥ l

∠2 = 90o

∴ ∠1 = ∠2 = 90o

But ∠1 and ∠2 are the corresponding angles made by the transversal l with lines m and n and they are proved to be equal.

Thus, m || n.

Question 1:

Exercise 4D

Since, sum of the angles of a triangle is 180o

∠A + ∠B + ∠C = 180o

⇒ ∠A + 76o + 48o = 180o

⇒ ∠A = 180o – 124o = 56o

∴ ∠A = 56o

Question 2:

Let the measures of the angles of a triangle are (2x)o, (3x)o and (4x)o. Then, 2x + 3x + 4x = 180 [sum of the angles of a triangle is 180o ]

⇒ 9x = 180

⇒ x =

= 20

∴ The measures of the required angles are: 2x = (2 × 20)o = 40o

3x = (3 × 20)o = 60o

4x = (4 × 20)o = 80o

Question 3:

Let 3∠A = 4∠B = 6∠C = x (say) Then, 3∠A = x

⇒ ∠A =

4∠B = x

⇒ ∠B =

and 6∠C = x

⇒ ∠C =

As ∠A + ∠B + ∠C = 180o

Question 4:

∠A + ∠B = 108o [Given]

But as ∠A, ∠B and ∠C are the angles of a triangle,

∠A + ∠B + ∠C = 180o

⇒ 108o + ∠C = 180o

⇒ C = 180o – 108o = 72o

Also, ∠B + ∠C = 130o [Given]

⇒ ∠B + 72o = 130o

⇒ ∠B = 130o – 72o = 58o Now as, ∠A + ∠B = 108o

⇒ ∠A + 58o = 108o

⇒ ∠A = 108o – 58o = 50o

∴ ∠A = 50o, ∠B = 58o and ∠C = 72o.

Question 5:

Since. ∠A , ∠B and ∠C are the angles of a triangle . So, ∠A + ∠B + ∠C = 180o

Now, ∠A + ∠B = 125o [Given]

∴ 125o + ∠C = 180o

⇒ ∠C = 180o – 125o = 55o

Also, ∠A + ∠C = 113o [Given]

⇒ ∠A + 55o = 113o

⇒ ∠A = 113o – 55o = 58o Now as ∠A + ∠B = 125o

⇒ 58o + ∠B = 125o

⇒ ∠B = 125o – 58o = 67o

∴ ∠A = 58o, ∠B = 67o and ∠C = 55o.

Question 6:

Since, ∠P, ∠Q and ∠R are the angles of a triangle. So, ∠P + ∠Q + ∠R = 180o ….(i)

Now, ∠P – ∠Q = 42o [Given]

⇒ ∠P = 42o + ∠Q ….(ii)

and ∠Q – ∠R = 21o [Given]

⇒ ∠R = ∠Q – 21o ….(iii)

Substituting the value of ∠P and ∠R from (ii) and (iii) in (i), we get,

⇒ 42o + ∠Q + ∠Q + ∠Q – 21o = 180o

⇒ 3∠Q + 21o = 180o

⇒ 3∠Q = 180o – 21o = 159o

∠Q =

= 53o

∴ ∠P = 42o + ∠Q

= 42o + 53o = 95o

∠R = ∠Q – 21o

= 53o – 21o = 32o

∴ ∠P = 95o, ∠Q = 53o and ∠R = 32o.

Question 7:

Given that the sum of the angles A and B of a ABC is 116o, i.e., ∠A + ∠B = 116o. Since, ∠A + ∠B + ∠C = 180o

So, 116o + ∠C = 180o

⇒ ∠C = 180o – 116o = 64o

Also, it is given that:

∠A – ∠B = 24o

⇒ ∠A = 24o + ∠B

Putting, ∠A = 24o + ∠B in ∠A + ∠B = 116o, we get,

⇒ 24o + ∠B + ∠B = 116o

⇒ 2∠B + 24o = 116o

⇒ 2∠B = 116o – 24o = 92o

∠B =

= 46o

Therefore, ∠A = 24o + 46o = 70o

∴ ∠A = 70o, ∠B = 46o and ∠C = 64o.

Question 8:

Let the two equal angles, A and B, of the triangle be xo each. We know,

∠A + ∠B + ∠C = 180o

⇒ xo + xo + ∠C = 180o

⇒ 2xo + ∠C = 180o ….(i) Also, it is given that,

∠C = xo + 18o ….(ii)

Substituting ∠C from (ii) in (i), we get,

⇒ 2xo + xo + 18o = 180o

⇒ 3xo = 180o – 18o = 162o x =

= 54o

Thus, the required angles of the triangle are 54o, 54o and xo + 18o = 54o + 18o = 72o.

Question 9:

Let ∠C be the smallest angle of ABC. Then, ∠A = 2∠C and B = 3∠C

Also, ∠A + ∠B + ∠C = 180o

⇒ 2∠C + 3∠C + ∠C = 180o

⇒ 6∠C = 180o

⇒ ∠C = 30o

So, ∠A = 2∠C = 2 (30o) = 60o

∠B = 3∠C = 3 (30o) = 90o

∴ The required angles of the triangle are 60o, 90o, 30o.

Question 10:

Let ABC be a right angled triangle and ∠C = 90o Since, ∠A + ∠B + ∠C = 180o

⇒ ∠A + ∠B = 180o – ∠C = 180o – 90o = 90o

Suppose ∠A = 53o

Then, 53o + ∠B = 90o

⇒ ∠B = 90o – 53o = 37o

∴ The required angles are 53o, 37o and 90o.

Question 11:

Let ABC be a triangle. Given, ∠A + ∠B = ∠C

We know, ∠A + ∠B + ∠C = 180o

⇒ ∠C + ∠C = 180o

⇒ 2∠C = 180o

⇒ ∠C =

= 90o

So, we find that ABC is a right triangle, right angled at C.

Question 12:

Given : ∆ABC in which ∠A = 90o, AL ⊥ BC To Prove: ∠BAL = ∠ACB

Proof :

In right triangle ∆ABC,

⇒ ∠ABC + ∠BAC + ∠ACB = 180o

⇒ ∠ABC + 90o + ∠ACB = 180o

⇒ ∠ABC + ∠ACB = 180o – 90o

∴ ∠ABC + ∠ACB = 90o

⇒ ∠ ACB = 90o – ∠ABC ….(1)

Similarly since ∆ABL is a right triangle, we find that,

∠BAL = 90o – ∠ABC …(2)

Thus from (1) and (2), we have

∴ ∠BAL = ∠ACB (Proved)

Question 13:

Let ABC be a triangle. So, ∠A < ∠B + ∠C

Adding A to both sides of the inequality,

⇒ 2∠A < ∠A + ∠B + ∠C

⇒ 2∠A < 180o

⇒ ∠A <

= 90o

[Since ∠A + ∠B + ∠C = 180o]

Similarly, ∠B < ∠A + ∠C

⇒ ∠B < 90o

and ∠C < ∠A + ∠B

⇒ ∠C < 90o

∆ABC is an acute angled triangle.

Question 14:

Let ABC be a triangle and ∠B > ∠A + ∠C Since, ∠A + ∠B + ∠C = 180o

⇒ ∠A + ∠C = 180o – ∠B Therefore, we get

∠B > 180o – ∠B

Adding ∠B on both sides of the inequality, we get,

⇒ ∠B + ∠B > 180o – ∠B + ∠B

⇒ 2∠B > 180o

⇒ ∠B >

= 90o

i.e., ∠B > 90o which means ∠B is an obtuse angle.

∆ABC is an obtuse angled triangle.

Question 15:

Since ∠ACB and ∠ACD form a linear pair. So, ∠ACB + ∠ACD = 180o

⇒ ∠ACB + 128o = 180o

⇒ ∠ACB = 180o – 128 = 52o

Also, ∠ABC + ∠ACB + ∠BAC = 180o

⇒ 43o + 52o + ∠BAC = 180o

⇒ 95o + ∠BAC = 180o

⇒ ∠BAC = 180o – 95o = 85o

∴ ∠ACB = 52o and ∠BAC = 85o.

Question 16:

As ∠DBA and ∠ABC form a linear pair. So, ∠DBA + ∠ABC = 180o

⇒ 106o + ∠ABC = 180o

⇒ ∠ABC = 180o – 106o = 74o

Also, ∠ACB and ∠ACE form a linear pair. So, ∠ACB + ∠ACE = 180o

⇒ ∠ACB + 118o = 180o

⇒ ∠ACB = 180o – 118o = 62o

In ∠ABC, we have,

∠ABC + ∠ACB + ∠BAC = 180o 74o + 62o + ∠BAC = 180o

⇒ 136o + ∠BAC = 180o

⇒ ∠BAC = 180o – 136o = 44o

∴ In triangle ABC, ∠A = 44o, ∠B = 74o and ∠C = 62o

Question 17:

(i) ∠EAB + ∠BAC = 180o [Linear pair angles]

110o + ∠BAC = 180o

⇒ ∠BAC = 180o – 110o = 70o

Again, ∠BCA + ∠ACD = 180o [Linear pair angles]

⇒ ∠BCA + 120o = 180o

⇒ ∠BCA = 180o – 120o = 60o

Now, in ∆ABC,

∠ABC + ∠BAC + ∠ACB = 180o

xo + 70o + 60o = 180o

⇒ x + 130o = 180o

⇒ x = 180o – 130o = 50o

∴ x = 50 (ii)

In ∆ABC,

∠A + ∠B + ∠C = 180o

⇒ 30o + 40o + ∠C = 180o

⇒ 70o + ∠C = 180o

⇒ ∠C = 180o – 70o = 110o

Now ∠BCA + ∠ACD = 180o [Linear pair]

⇒ 110o + ∠ACD = 180o

⇒ ∠ACD = 180o – 110o = 70o In ∆ECD,

⇒ ∠ECD + ∠CDE + ∠CED = 180o

⇒ 70o + 50o + ∠CED = 180o

⇒ 120o + ∠CED = 180o

∠CED = 180o – 120o = 60o

Since ∠AED and ∠CED from a linear pair So, ∠AED + ∠CED = 180o

⇒ xo + 60o = 180o

⇒ xo = 180o – 60o = 120o

∴ x = 120 (iii)

∠EAF = ∠BAC [Vertically opposite angles]

⇒ ∠BAC = 60o

In ∆ABC, exterior ∠ACD is equal to the sum of two opposite interior angles. So, ∠ACD = ∠BAC + ∠ABC

⇒ 115o = 60o + xo

⇒ xo = 115o – 60o = 55o

∴ x = 55 (iv)

Since AB || CD and AD is a transversal. So, ∠BAD = ∠ADC

⇒ ∠ADC = 60o

In ∠ECD, we have,

∠E + ∠C + ∠D = 180o

⇒ xo + 45o + 60o = 180o

⇒ xo + 105o = 180o

⇒ xo = 180o – 105o = 75o

∴ x = 75 (v)

In ∆AEF,

Exterior ∠BED = ∠EAF + ∠EFA

⇒ 100o = 40o + ∠EFA

⇒ ∠EFA = 100o – 40o = 60o

Also, ∠CFD = ∠EFA [Vertically Opposite angles]

⇒ ∠CFD = 60o Now in ∆FCD,

Exterior ∠BCF = ∠CFD + ∠CDF

⇒ 90o = 60o + xo

⇒ xo = 90o – 60o = 30o

∴ x = 30 (vi)

In ∆ABE, we have,

∠A + ∠B + ∠E = 180o

⇒ 75o + 65o + ∠E = 180o

⇒ 140o + ∠E = 180o

⇒ ∠E = 180o – 140o = 40o

Now, ∠CED = ∠AEB [Vertically opposite angles]

⇒ ∠CED = 40o

Now, in ∆CED, we have,

∠C + ∠E + ∠D = 180o

⇒ 110o + 40o + xo = 180o

⇒ 150o + xo = 180o

⇒ xo = 180o – 150o = 30o

∴ x = 30

Question 18:

Produce CD to cut AB at E.

Now, in ∆BDE, we have,

Exterior ∠CDB = ∠CEB + ∠DBE

⇒ xo = ∠CEB + 45o In ∆AEC, we have,

…..(i)

Exterior ∠CEB = ∠CAB + ∠ACE

= 55o + 30o = 85o

Putting ∠CEB = 85o in (i), we get, xo = 85o + 45o = 130o

∴ x = 130

Question 19:

The angle ∠BAC is divided by AD in the ratio 1 : 3. Let ∠BAD and ∠DAC be y and 3y, respectively. As BAE is a straight line,

∠BAC + ∠CAE = 180o

[linear pair]

⇒ ∠BAD + ∠DAC + ∠CAE = 180o

⇒ y + 3y + 108o = 180o

⇒ 4y = 180o – 108o = 72o

⇒ y =

= 18o Now, in ∆ABC,

∠ABC + ∠BCA + ∠BAC = 180o

y + x + 4y = 180o

[Since, ∠ABC = ∠BAD (given AD = DB) and ∠BAC = y + 3y = 4y]

⇒ 5y + x = 180

⇒ 5 × 18 + x = 180

⇒ 90 + x = 180

∴ x = 180 – 90 = 90

Question 20:

Given : A ∆ABC in which BC, CA and AB are produced to D, E and F respectively. To prove : Exterior ∠DCA + Exterior ∠BAE + Exterior ∠FBD = 360o

Proof : Exterior ∠DCA = ∠A + ∠B ….(i) Exterior ∠FAE = ∠B + ∠C ….(ii) Exterior ∠FBD = ∠A + ∠C ….(iii) Adding (i), (ii) and (iii), we get,

Ext. ∠DCA + Ext. ∠FAE + Ext. ∠FBD

= ∠A + ∠B + ∠B + ∠C + ∠A + ∠C

= 2∠A + 2∠B + 2∠C

= 2 (∠A + ∠B + ∠C)

= 2 × 180o

[Since, in triangle the sum of all three angle is 180o]

= 360o

Hence, proved.

Question 21:

In ∆ACE, we have,

∠A + ∠C + ∠E = 180o ….(i) In ∆BDF, we have,

∠B + ∠D + ∠F = 180o ….(ii)

Adding both sides of (i) and (ii), we get,

∠A + ∠C +∠E + ∠B + ∠D + ∠F = 180o + 180o

⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360o.

Question 22:

Given : In ∆ABC, bisectors of ∠B and ∠C meet at O and ∠A = 70o In ∆BOC, we have,

∠BOC + ∠OBC + ∠OCB = 180o

= 180o – 55o = 125o

∴ ∠BOC = 125o.

Question 23:

We have a ∆ABC whose sides AB and AC have been procued to D and E. A = 40o and bisectors of ∠CBD and ∠BCE meet at O.

In ∆ABC, we have, Exterior ∠CBD = C + 40o

And exterior ∠BCE = B + 40o

Now, in ∆BCO, we have,

= 50o + 20o

= 70o

Thus, ∠BOC = 70o

Question 24:

In the given ∆ABC, we have,

∠A : ∠B : ∠C = 3 : 2 : 1

Let ∠A = 3x, ∠B = 2x, ∠C = x. Then,

∠A + ∠B + ∠C = 180o

⇒ 3x + 2x + x = 180o

⇒ 6x = 180o

⇒ x = 30o

∠A = 3x = 3 30o = 90o

∠B = 2x = 2 30o = 60o

and, ∠C = x = 30o

Now, in ∆ABC, we have,

Ext ∠ACE = ∠A + ∠B = 90o + 60o = 150o

∠ACD + ∠ECD = 150o

⇒ ∠ECD = 150o – ∠ACD

⇒ ∠ECD = 150o – 90o

⇒ ∠ECD= 60o

[since , AD ⊥ CD, ∠ACD = 90o]

Question 25:

In ∆ABC, AN is the bisector of ∠A and AM ⊥ BC. Now in ∆ABC we have;

∠A = 180o – ∠B – ∠C

⇒ ∠A = 180o – 65o – 30o

= 180o – 95o

= 85o

Now, in ∆ANC we have;

Thus, ∠MAN =

Question 26:

(i) False (ii) True (iii) False (iv) False (v) True (vi) True.