Imaginary Quantity
The square root of a negative real number is called an imaginary quantity or imaginary number. e.g., √-3, √-7/2
The quantity √-1 is an imaginary number, denoted by ‘i’, called iota.
Integral Powers of Iota (i)
i=√-1, i2 = -1, i3 = -i, i4=1
So, i4n+1= i, i4n+2 = -1, i4n+3 = -i, i4n+4 = i4n = 1
In other words,
in = (-1)n/2, if n is an even integer
in = (-1)(n-1)/2.i, if is an odd integer
Complex Number
A number of the form z = x + iy, where x, y ∈ R, is called a complex number
The numbers x and y are called respectively real and imaginary parts of complex number z.
i.e., x = Re (z) and y = Im (z)
Purely Real and Purely Imaginary Complex Number
A complex number z is a purely real if its imaginary part is 0.
i.e., Im (z) = 0. And purely imaginary if its real part is 0 i.e., Re (z)= 0.
Equality of Complex Numbers
Two complex numbers z1 = a1 + ib1 and z2 = a2 + ib2 are equal, if a2= a2 and b1 = b2 i.e., Re (z1) = Re (z2) and Im (z1) = Im (z2).
Algebra of Complex Numbers
1. Addition of Complex Numbers
Let z1 = (x1 + iyi) and z2 = (x2 + iy2) be any two complex numbers, then their sum defined as
z1 + z2 = (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2)
Properties of Addition
(i) Commutative z1 + z2 = z2 + z1
(ii) Associative (z1 + z2) + z3 = + (z2 + z3)
(iii) Additive Identity z + 0 = z = 0 + z
Here, 0 is additive identity.
2. Subtraction of Complex Numbers
Let z1 = (x1 + iy1) and z2 = (x2 + iy2) be any two complex numbers, then their difference is defined as
z1 – z2 = (x1 + iy1) – (x2 + iy2)
= (x1 – x2) + i(y1 – y2)
3. Multiplication of Complex Numbers
Let z1 = (x1 + iyi) and z2 = (x2 + iy2) be any two complex numbers, then their multiplication is defined as
z1z2 = (x1 + iy1)(x2 + iy2) = (x1x2 – y1y2) + i(x1y2 + x2y1)
Properties of Multiplication
(i) Commutative z1z2 = z2z1
(ii) Associative (z1 z2) z3 = z1(z2 z3)
(iii) Multiplicative Identity z • 1 = z = 1 • z
Here, 1 is multiplicative identity of an element z.
(iv) Multiplicative Inverse Every non-zero complex number z there exists a complex number z1 such that z.z1 = 1 = z1 • z
(v) Distributive Law
(a) z1(z2 + z3) = z1z2 + z1z3 (left distribution)
(b) (z2 + z3)z1 = z2z1 + z3z1 (right distribution)
4. Division of Complex Numbers
Let z1 = x1 + iy1 and z2 = x2 + iy2 be any two complex numbers, then their division is defined as
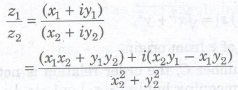
where z2 # 0.
Conjugate of a Complex Number
If z = x + iy is a complex number, then conjugate of z is denoted by z
i.e., z = x – iy
Properties of Conjugate

Modulus of a Complex Number
If z = x + iy, , then modulus or magnitude of z is denoted by |z| and is given by
|z| = x2 + y2.
It represents a distance of z from origin.
In the set of complex number C, the order relation is not defined i.e., z1> z2 or zi <z2 has no meaning but |z1|>|z2| or |z1|< | z2 | has got its meaning, since |z| and |z2| are real numbers.
Properties of Modulus

Reciprocal/Multiplicative Inverse of a Complex Number
Let z = x + iy be a non-zero complex number, then
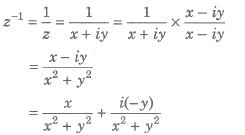
Here, z-1 is called multiplicative inverse of z.
Argument of a Complex Number
Any complex number z=x+iy can be represented geometrically by a point (x, y) in a plane, called Argand plane or Gaussian plane. The angle made by the line joining point z to the origin, with the x-axis is called argument of that complex number. It is denoted by the symbol arg (z) or amp (z).
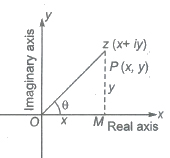
Argument (z) = θ = tan-1(y/x)
Argument of z is not unique, general value of the argument of z is 2nπ + θ. But arg (0) is not defined.
A purely real number is represented by a point on x-axis.
A purely imaginary number is represented by a point on y-axis.
There exists a one-one correspondence between the points of the plane and the members of the set C of all complex numbers.
The length of the line segment OP is called the modulus of z and is denoted by |z|.
i.e., length of OP = √x2 + y2.
Principal Value of Argument
The value of the argument which lies in the interval (- π, π] is called principal value of argument.
(i) If x> 0 and y > 0, then arg (z) = 0
(ii) If x < 0 and y> 0, then arg (z) = π -0
(iii) If x < 0 and y < 0, then arg (z) = – (π – θ)
(iv) If x> 0 and y < 0, then arg (z) = -θ
Properties of Argument
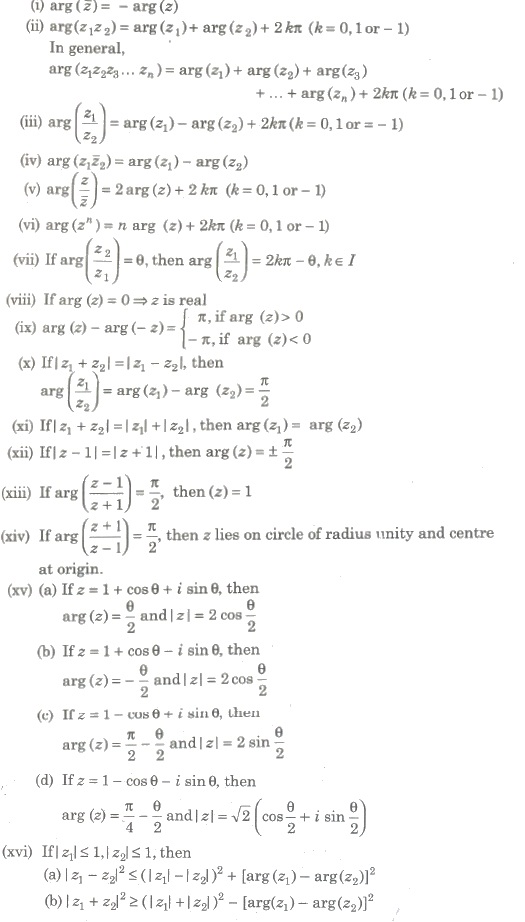
Square Root of a Complex Number
If z = x + iy, then
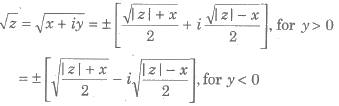
Polar Form
If z = x + iy is a complex number, then z can be written as
z = |z| (cos θ + i sin θ) where, θ = arg (z)
this is called polar form.
If the general value of the argument is 0, then the polar form of z is
z = |z| [cos (2nπ + θ) + i sin (2nπ + θ)], where n is an integer.
Eulerian Form of a Complex Number
If z = x + iy is a complex number, then it can be written as
z = rei0, where
r = |z| and θ = arg (z)
This is called Eulerian form and ei0= cosθ + i sinθ and e-i0 = cosθ — i sinθ.
De-Moivre’s Theorem
A simplest formula for calculating powers of complex number known as De-Moivre’s theorem.
If n ∈ I (set of integers), then (cosθ + i sinθ)n = cos nθ + i sin nθ and if n ∈ Q (set of rational numbers), then cos nθ + i sin nθ is one of the values of (cos θ + i sin θ)n.
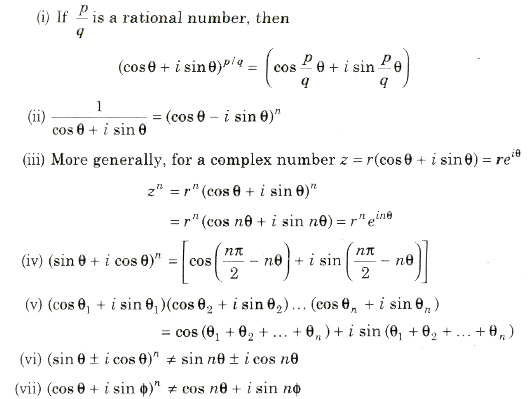
The nth Roots of Unity
The nth roots of unity, it means any complex number z, which satisfies the equation zn = 1 or z = (1)1/n
or z = cos(2kπ/n) + isin(2kπ/n) , where k = 0, 1, 2, … , (n — 1)
Properties of nth Roots of Unity
- nth roots of unity form a GP with common ratio e(i2π/n) .
- Sum of nth roots of unity is always 0.
- Sum of nth powers of nth roots of unity is zero, if p is a multiple of n
- Sum of pth powers of nth roots of unity is zero, if p is not a multiple of n.
- Sum of pth powers of nth roots of unity is n, ifp is a multiple of n.
- Product of nth roots of unity is (-1)(n – 1).
- The nth roots of unity lie on the unit circle |z| = 1 and divide its circumference into n equal parts.
The Cube Roots of Unity
Cube roots of unity are 1, ω, ω2,
where ω = -1/2 + i√3/2 = e(i2π/3) and ω2 = (-1 – i√3)/2
ω3r + 1 = ω, ω3r + 2 = ω2
Properties of Cube Roots of Unity
(i) 1 + ω + ω2r =
0, if r is not a multiple of 3.
3, if r is,a multiple of 3.
(ii) ω3 = ω3r = 1
(iii) ω3r + 1 = ω, ω3r + 2 = ω2
(iv) Cube roots of unity lie on the unit circle |z| = 1 and divide its circumference into 3 equal parts.
(v) It always forms an equilateral triangle.
(vi) Cube roots of – 1 are -1, – ω, – ω2.

Geometrical Representations of Complex Numbers
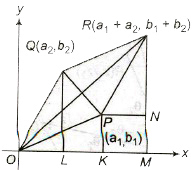
1. Geometrical Representation of Addition
If two points P and Q represent complex numbers z1 and z2 respectively, in the Argand plane, then the sum z1 + z2 is represented
by the extremity R of the diagonal OR of parallelogram OPRQ having OP and OQ as two adjacent sides.
2. Geometrical Representation of Subtraction
Let z1 = a1 + ib1 and z2 = a2 + ia2 be two complex numbers represented by points P (a1, b1) and Q(a2, b2) in the Argand plane. Q’ represents the complex number (—z2). Complete the parallelogram OPRQ’ by taking OP and OQ’ as two adjacent sides.
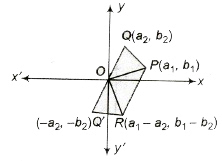
The sum of z1 and —z2 is represented by the extremity R of the diagonal OR of parallelogram OPRQ’. R represents the complex number z1 — z2.
3. Geometrical Representation of Multiplication of Complex Numbers
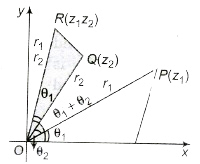
R has the polar coordinates (r1r2, θ1 + θ2) and it represents the complex numbers z1z2.
4. Geometrical Representation of the Division of Complex Numbers
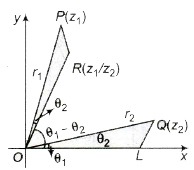
R has the polar coordinates (r1/r2, θ1 – θ2) and it represents the complex number z1/z2.
|z|=|z| and arg (z) = – arg (z). The general value of arg (z) is 2nπ – arg (z).
If a point P represents a complex number z, then its conjugate i is represented by the image of P in the real axis.
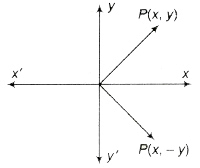
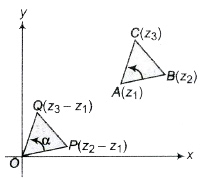
Concept of Rotation
Let z1, z2 and z3 be the vertices of a ΔABC described in anti-clockwise sense. Draw OP and OQ parallel and equal to AB and AC, respectively. Then, point P is z2 – z1 and Q is z3 – z1. If OP is rotated through angle a in anti-clockwise, sense it coincides with OQ.
Important Points to be Remembered
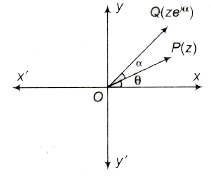
(a) zeiα a is the complex number whose modulus is r and argument θ + α.
(b) Multiplication by e-iα to z rotates the vector OP in clockwise sense through an angle α.
(ii) If z1, z2, z3 and z4 are the affixes of the points A, B,C and D, respectively in the Argand plane.
(a) AB is inclined to CD at the angle arg [(z2 – z1)/(z4 – z3)].
(b) If CD is inclines at 90° to AB, then arg [(z2 – z1)/(z4 – z3)] = ±(π/2).
(c) If z1 and z2 are fixed complex numbers, then the locus of a point z satisfying arg [([(z – z1)/(z – z2)] = ±(π/2).
Logarithm of a Complex Number
Let z = x + iy be a complex number and in polar form of z is reiθ , then
log(x + iy) = log (reiθ) = log (r) + iθ
log(√x2 + y2) + itan-1 (y/x)
or log(z) = log (|z|)+ iamp (z),
In general,
z = rei(θ + 2nπ)
log z = log|z| + iarg z + 2nπi
Applications of Complex Numbers in Coordinate Geometry
Distance between complex Points
(i) Distance between A(z1) and B(1) is given by
AB = |z2 — z1| = √(x2 + x1)2 + (y2 + y1)2
where z1 = x1 + iy1 and z2 = x2 + iy2
(ii) The point P (z) which divides the join of segment AB in the ratio m : n is given by
z = (mz2 + nz1)/(m + n)
If P divides the line externally in the ratio m : n, then
z = (mz2 – nz1)/(m – n)
Triangle in Complex Plane
(i) Let ABC be a triangle with vertices A (z1), B(z2) and C(z3 ) then
(a) Centroid of the ΔABC is given by
z = 1/3(z1 + z2 + z3)
(b) Incentre of the AABC is given by
z = (az1 + bz2 + cz3)/(a + b + c)
(ii) Area of the triangle with vertices A(z1), B(z2) and C(z3) is given by
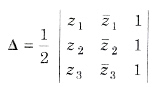
For an equilateral triangle,
z12 + z22 + z32 = z2z3 + z3z1 + z1z2
(iii) The triangle whose vertices are the points represented by complex numbers z1, z2 and z3 is equilateral, if

Straight Line in Complex Plane
(i) The general equation of a straight line is az + az + b = 0, where a is a complex number and b is a real number.
(ii) The complex and real slopes of the line az + az are -a/a and – i[(a + a)/(a – a)].
(iii) The equation of straight line through z1 and z2 is z = tz1 + (1 — t)z2, where t is real.
(iv) If z1 and z2 are two fixed points, then |z — z1| = z — z2| represents perpendicular bisector of the line segment joining z1 and z2.
(v) Three points z1, z2 and z3 are collinear, if
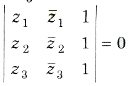
This is also, the equation of the line passing through 1, z2 and z3 and slope is defined to be (z1 – z2)/z1 – z2
(vi) Length of Perpendicular The length of perpendicular from a point z1 to az + az + b = 0 is given by |az1 + az1 + b|/2|a|
(vii) arg (z – z1)/(z – z2) = β
Locus is the arc of a circle which the segment joining z1 and z2 as a chord.
(viii) The equation of a line parallel to the line az + az + b = 0 is az + az + λ = 0, where λ ∈ R.
(ix) The equation of a line parallel to the line az + az + b = 0 is az + az + iλ = 0, where λ ∈ R.
(x) If z1 and z2 are two fixed points, then I z — z11 =I z z21 represents perpendicular bisector of the segment joining A(z1) and B(z2).
(xi) The equation of a line perpendicular to the plane z(z1 – z2) + z(z1 – z2) = |z1|2 – |z2|2.
(xii) If z1, z2 and z3 are the affixes of the points A, B and C in the Argand plane, then
(a) ∠BAC = arg[(z3 – z1/z2 – z1)]
(b) [(z3 – z1)/(z2 – z1)] = |z3 – z1|/|z2 – z1| (cos α + isin α), where α = ∠BAC.
(xiii) If z is a variable point in the argand plane such that arg (z) = θ, then locus of z is a straight line through the origin inclined at an angle θ with X-axis.
(xiv) If z is a variable point and z1 is fixed point in the argand plane such that (z — z1)= θ, then locus of z is a straight line passing through the point z1 and inclined at an angle θ with the X-axis.
(xv) If z is a variable point and z1, z2 are two fixed points in the Argand plane, then
(a) |z – z1| + |z – z2| = |z1– z2|
Locus of z is the line segment joining z1 and z2.
(b) |z – z1| – |z – z2| = |z1– z2|
Locus of z is a straight line joining z1 and z2 but z does not lie between z1 and z2.
(c) arg[(z – z1)/(z – z2)] = 0 or π
Locus z is a straight line passing through z1 and z2.
(d) |z – z1|2 + |z – z2|2 = |z1 – z2|2
Locus of z is a circle with z1 and z2 as the extremities of diameter.
Circle in Complete Plane
(i) An equation of the circle with centre at z0 and radius r is
|z – z0| = r
or zz – z0z – z0z + z0
- |z — z0| < r, represents interior of the circle.
- |z — z0| > r, represents exterior of the circle.
- |z — z0| ≤ r is the set of points lying inside and on the circle |z — z0| = r. Similarly, |z — z0| ≥ r is the set of points lying outside and on the circle |z — z0| = r.
- General equation of a circle is
zz – az – az + b = 0
where a is a complex number and b is a real number. Centre of the circle = – a
Radius of the circle = √aa – b or √|a|2 – b
(a) Four points z1, z2, z3 and z4 are concyclic, if
[(z4 — z1)(z2 — z3)]/[(z4 – z3)(z2 – z1)] is purely real.
(ii) |z — z1|/|z – z2| = k ⇒ Circle, if k ≠ 1 or Perpendicular bisector, if k = 1
(iii) The equation of a circle described on the line segment joining z1 and 1 as diameter is (z – z1) (z – z2) + (z – z2) (z — z1) = 0
(iv) If z1, and z2 are the fixed complex numbers, then the locus of a point z satisfying arg [(z – z1)/(z – z2)] = ± π / 2 is a circle having z1 and z2 at the end points of a diameter.
Conic in Complex plane
(i) Let z1 and z2 be two fixed points, and k be a positive real number.
If k >|z1– z2|, then |z – z1| + |z – z2| = k represents an ellipse with foci at A(z1) and B(z2) and length of the major axis is k.
(ii) Let z1 and z2 be two fixed points and k be a positive real number.
If k ≠ |z1– z2| , then |z – z1| – |z – z2| = k represents hyperbola with foci at A(z1) and B(z2).
Important Points to be Remembered
- √-a x √-b ≠ √ab
√a x √b = √ab is possible only, if both a and b are non-negative.
So, i2 = √-1 x √-1 ≠ √1
- is neither positive, zero nor negative.
- Argument of 0 is not defined.
- Argument of purely imaginary number is π/2
- Argument of purely real number is 0 or π.
- If |z + 1/z| = a then the greatest value of |z| = a + √a2 + 4/2 and the least value of |z| = -a + √a2 + 4/2
- The value of ii = e-π2
- The complex number do not possess the property of order, i.e., x + iy < (or) > c + id is not defined.
- The area of the triangle on the Argand plane formed by the complex numbers z, iz and z + iz is 1/2|z|2.
- (x) If ω1 and ω2 are the complex slope of two lines on the Argand plane, then the lines are
(a) perpendicular, if ω1 + ω2 = 0.
(b) parallel, if ω1 = ω2.