Coordinate Geometry
The branch of Mathematics in which geometrical problem are solved through algebra by using the coordinate system, is known as coordinate geometry.
Rectangular Axis
Let XOX’ and YOY’ be two fixed straight lines, which meet at right angles at O. Then,
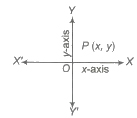
(i) X’OX is called axis of X or the X-axis or abscissa.
(ii) Y’OY is called axis of Yor the Y-axis or ordinate.
(iii) The ordered pair of real numbers (x, y) is called cartesian coordinate .
Quadrants
The X and Y-axes divide the coordinate plane into four parts, each part is called a quadrant which is given below.

Polar Coordinates
In ΔOPQ,

cos θ = x / r and sin θ = y / r ⇒ x = r cos θ and y = r sin θ
where, r = √x2 + y2
The polar coordinate is represented by the symbol P(r,θ).
Distance Formula
(i) Distance between two points P (x1, y1) and Q (x2, y2), is
√(x2 – x1)2 + (y2 – y1)2.

(ii) If points are (r1 , θ1) arid (r2, θ2), then distance between them is
√r21 + r22 – 2r1r2cos(θ1 – θ2).
(iii) Distance of a point (x1, y1) from the origin is √x21 + y21.
Section Formula
(i) The coordinate of the point which divides the joint of (x1, y1) and (x2, y2) in the ratio m1: m2 internally, is
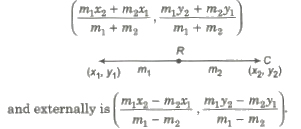
(ii) X-axis divides the line segment joining (x1, y1) and (x2, y2) in the ratio – y1 : y2.
Similarly, Y-axis divides the same line segment in the ratio – x1 : x2.
(iii) Mid-point of the joint of (x1, y1) and (x2, y2) is (x1 + x2 / 2 , y1 + y2 / 2)
(iv) Centroid of ΔABC with vertices (x1, y1), (x2, y2) and (x3, y3), is
(x1 + x2 + x3 / 3 , y1 + y2 + y3 / 3).
(v) Circumcentre of ΔABC with vertices A(x1, y1), B(x2, y2) and C(x3, y3), is
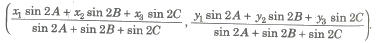
(vi) Incentre of Δ ABC with vertices A(x1, y1), B(x2, y2) and C(x3, y3) and whose sides are a, band c, is
(ax1 + bx2 + cx3 / a + b + c , ay1 + by2 + cy3 / a + b + c).
(vii) Excentre of ΔABC with vertices A(x1, y1), B(x2, y2) and C(x3, y3) and whose sides are a, band c, is given by
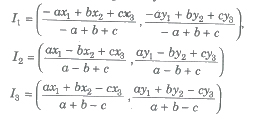
Area of Triangle/Quadrilateral
(i) Area of ΔABC with vertices A(x1, y1), B(x2, y2) and C(x3, y3), is

These points A, Band C will be collinear, if Δ = O.
(ii) Area of the quadrilateral formed by joining the vertices
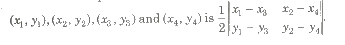
(iii) Area of trapezium formed by joining the vertices
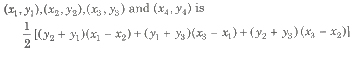
Shifting/Rotation of Origin/Axes
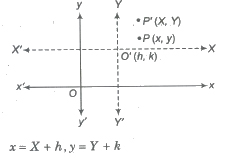
Shifting of Origin
Let the origin is shifted to a point O'(h, k). If P(x, y) are coordinates of a point referred to old axes and P’ (X, Y) are the coordinates of the same points referred to new axes, then
Rotation of Axes
Let (x, y) be the coordinates of any point P referred to the old axes and (X, Y) be its coordinates referred to the new axes (after rotating the old axes by angle θ). Then,
X = x cos θ + y sin θ and Y = y cos θ + x sin θ

Shifting of Origin and Rotation of Axes
If origin is shifted to point (h, k) and system is also rotated by an angle θ in anti-clockwise, then coordinate of new point P’ (x’, y’) is obtained by replacing
x’= h + x cos θ + y sin θ
and y’ = k – x sin θ + y cos θ
Locus
The curve described by a point which moves under given condition(s) is called its locus.
Equation of Locus
The equation of the locus of a point which is satisfied by the coordinates of every point.
Algorithm to Find the Locus of a Point
Step I Assume the coordinates of the point say (h,k) whose locus is to be found.
Step II Write the given condition in mathematical form involving h, k.
Step III Eliminate the variable(s), if any.
Step IV Replace h by x and k by y in the result obtained in step III. The equation so obtained is the locus of the point, which moves under some stated condition(s).
Straight Line
Any curve is said to be a straight line, if two points are taken on the curve such that every point on the line segment joining any two points on it lies on the curve.
General equation of a line is ax + by + c = o.
Slope (Gradient) of a Line )
The trigonometric tangent of the angle that a line makes with the positive direction of the X-axis in anti-clockwise sense is called the slope or gradient of the line.
So, slope of a line, m = tan θ
where, θ is the angle made by the line with positive direction of X-axis.
Important Results on Slope of Line
(i) Slope of a line parallel to X-axis, m = 0.
(ii) Slope of a line parallel to Y-axis, m = ∞.
(iii) Slope of a line equally inclined with axes is 1 or -1 as it makes an angle of 45° or 135°, with X-axis.
(iV) Slope of a line passing through (x, y,) and (x2, y2) is given by
m = tan θ = y2 – y1 / x2 – x1.
Angle between Two Lines
The angle e between two lines having slopes m1 and m2 is

(i) Two lines are parallel, iff m1 = m2.
(ii) Two lines are perpendicular to each other, iff m1m2 = – 1.
Equation of a Straight Line
General equation of a straight line is Ax + By + C = 0.
(i) The equation of a line parallel to X-axis at a distance b from it, is given by
y = b
(ii) The equation of a line parallel to Y-axis at a distance a from it, is given by
x = a
(iii) Equation of X-axis is
y = 0
(iv) Equation of Y-axis is
x = 0
Different Form of the Equation of a Straight Line
(i) Slope Intercept Form The equation of a line with slope m and making an intercept c on Y-axis, is
y = mx + c
If the line passes through the origin, then its equation will be
y= mx
(ii) One Point Slope Form The equation of a line which passes through the point (x1, y1) and has the slope of m is given by
(y – y1) = m (x – x1)
(iii) Two Points Form The equation of a line’ passing through the points (x1, y1) and (x2, y2) is given by
(y – y1) = (y2 – y1 / x2 – x1) (x – x1)
This equation can also be determined by the determinant method, that is
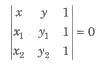
(iv) The Intercept Form The equation of a line which cuts off intercept a and b respectively on the X and Y-axes is given by
x / a + y / b = 1
The general equation Ax + By + C = 0 can be converted into the intercept form, as
x / – (C A) + y / – (C B) = 1
(v) The Normal Form The equation of a straight line upon which the length of the perpendicular from the origin is p and angle made by this perpendicular to the X-axis is α, is given by
x cos α + Y sin α = p

(vi) The Distance (Parametric) Form The equation of a straight line passing through (x1, y1) and making an angle θ with the positive direction of x-axis, is
x – x1 / cos θ = y – y1 / sin θ = r
where, r is the distance between two points P(x, y) and Q(x1, y1).
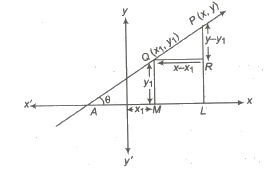
Thus, the coordinates of any point on the line at a distance r from the given point (x1, y1) are (x1 + r cos θ, y1 + r sin θ). If P is on the right side of (x1, y1) then r is positive and if P is on the left side of (x1, y1) then r is negative.
Position of Point(s) Relative to a Given Line
Let the equation of the given line be ax + by + C = 0 and let the Coordinates of the two given points be P(x1, y1) and Q(x2, y2).
(i) The two points are on the same side of the straight line ax + by + c = 0, if ax1 + by1 + c and ax2 + by2 + c have the same sign.
(ii) The two points are on the opposite side of the straight line ax + by + c = 0, if ax1 + by1 + c and ax2 + by2 + c have opposite sign.
(iii) A point (x1, y1) will lie on the side of the origin relative to a line ax + by + c = 0, if ax1+ by1 + c and c have the same sign.
(iv) A point (x1, y1) will lie on the opposite side of the origin relative to a line ax + by + c = 0, if ax1 + by1 + c and c have the opposite sign.
(v) Condition of concurrency for three given lines ax1 + by1 + c1 = 0, ax2 + by2 + c2 and ax3 + by3 + c3 = 0 is a3(b1c2 – b2c1) + b3(c1a2 – a1c2) + c3(a1b2 – a2b1) = 0
or
(vi) Point of Intersection of Two Lines Let equation of lines be ax1 + by1 + c1 = 0 and ax2 + by2 + c2 = 0, then their point of intersection is
(b1c2 – b2c1 / a1b2 – a2b1, c1a2 – c2a1 / a1b2 – a2b1).
Line Parallel and Perpendicular to a Given Line
(i) The equation of a line parallel to a given line ax + by + c = 0 is ax + by + λ = 0, where λ is a constant.
(ii) The equation of a line perpendicular to a given line ax + by + c = is bx – ay + λ = 0, where λ is a constant.
Image of a Point with Respect to a Line
Let the image of a point (x1, y1) with respect to ax + by + c = 0 be (x2, y2), then
x2 – x1 / a = y2 – y1 / b = – 2 (ax1 + by1 + c) / a2 + b2
(i) The image of the point P(x1, y1) with respect to X-axis is Q(x1 – y1).
(ii) The image of the point P(x1, y1) with respect to Y-axis is Q(-x1, y1).
(iii) The image of the point P(x1, y1) with respect to mirror Y = x is Q(y1, x1).
(iv) The image. of the point P(x1, y1) with respect to the line mirror y == x tan θ is
x = x1 cos 2θ + y1 sin 2θ
Y = x1 sin 2θ – y1 cos 2θ
(v) The image of the point P(x1, y1) with respect to the origin is the point (-x1, y1).
(vi) The length of perpendicular from a point (x1, y1) to a line ax + by + c = 0 is
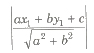
Equation of the Bisectors
The equation of the bisectors of the angle between the lines
a1x + b1y + c1 = 0
and a2x + b2y + c2 = 0
are given by
a1x + b1y + c1 / √a21 + b21 = ± a2x + b2y + c2 / √a22 + b22
(i) If a1 a2 + b1 b2 > 0, then we take positive sign for obtuse and negative sign for acute.
(ii) If a1 a2 + b1 b2 < 0, then we take negative sign for obtuse and positive sign for acute .
Pair of Lines
General equation of a pair of straight lines is ax2 + 2hxy + by2 + 2gx + 2fy + c = 0.
Homogeneous Equation of Second Degree
A rational, integral, algebraic equation in two variables x and y is said to be a homogeneous equation of the second degree, if the sum of the indices of x and y in each term is equal to 2.
The general form of homogeneous equation of the second degree x and y is ax2 + 2hxy + by2 = 0, which passes through the origin.
Important Properties
If ax2 + 2hxy + by2 = 0 be an equation of pair of straight lines.
(i) Slope of first line, m1 = – h + √h2 – ab / b
and slope of second line, m2 = – h – √h2 – ab / b
m1 + m2 = – 2h / b = – Coefficient of xy / Coefficient of y2
and m1 m2 = a / b = Coefficient of x2 / Coefficient of y2
Here, m1 and m2 are
(a) real and distinct, if h2 > ab.
(b) coincident, if h2 = ab.
(c) imaginary, if h2 < ab.
(ii) Angle between the pair of lines is given by
tan θ = 2√h2 – ab / a + b
(a) If lines are coincident, then h2 = ab
(b) If lines are perpendicular, then a + b = o.
(iii) The joint equation of bisector of the angles between the lines represented by the equation ax2 + 2hxy + by2 = 0 is
x2 – b2 / a – b = xy / h ⇒ hx2 – (a – b)xy – hy2=0.
(iv) The necessary and sufficient condition ax2 + 2hxy + by2 + 2gx + 2fy + C = 0 to represent a pair of straight lines, if abc + 2fgh – af2 – bg2 – ch2 = 0
or
(v) The equation of the bisectors of the angles between the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 are given by
(x – x1)2 – (y – y1)2 / a – b = (x – x1) (y – y1) / h,
where, (x1, y1) is the point of intersection of the lines represented by the given equation.
(vi) The general equation ax2 + 2hxy + by2 + 2gx + 2fy + C = 0 will represent two parallel lines, if g2 – ac > 0 and a / h = h / b = g / f and the distance between them is 2√g2 – ac / a(a + b) or 2√f2 – bc / b(a + b).
(vii) If the equation of a pair of straight lines is ax2 + 2hxy + by2 + 2gx + 2fy + C = 0, then the point of intersection is given by
(hf – bg / ab – h2, gh – af / ab – h2).
(viii) The equation of the pair of lines through the origin and perpendicular to the pair of lines given by ax2 + 2hxy + by2 = 0 is bx2 – 2hxy + ay2 = 0.
(ix) Equation of the straight lines having the origin to the points of intersection of a second degree curve ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 and a straight line Lx + my + n = 0 is
ax2 + 2hxy + by2 + 2gx(Lx + my / – n) + 2fy(Lx + my / – n) + c (Lx + my / – n)2 = 0.
Important Points to be Remembered
1. A triangle is an isosceles, if any two of its median are equal.
2. In an equilateral triangle, orthocentre, centroid, circumcentre, incentre coincide.
3. The circumcentre of a right angled triangle is the mid-point of the hypotenuse.
4. Orthocentre, centroid, circumcentre of a triangle are collinear, Centroid divides the line joining orthocentre and circumcentre in the ratio 2: 1.
5. If D, E and F are the mid-point of the sides BC, CA and AB of MBC, then the centroid of Δ ABC = centroid of Δ DEF.
6. Orthocentre of the right angled Δ ABC, right angled at A is A
7. Circumcentre of the right angled Δ ABC, right angled at A is B + C / 2.
8. The distance of a point (x1, y1) from the ax + by + c = 0 is
d = |ax1 + by1 + c / √a2 + b2|
9. Distance between two parallel lines a1x + b1y + c1 = 0 and a1x + b1y + c2 = 0 is given by
d = |c2 – c1 / √a2 + b2|.
10. The area of the triangle formed by the lines y =m1x + c1, y = m2x + c2 and y = m3x + c3 is .
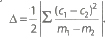 .
.
11. Area of the triangle formed by the line ax + by + c = 0 with the coordinate axes is Δ = c2 / 2|ab|.
12. The foot of the perpendicular(h,k) from (x1, y1) to the line ax + by + c = 0 is given by h – x1 / a = k – y1 / b = – (ax1 + by1 + c) / a2 + b2.
13. Area of rhombus formed by ax ± by ± c = 0 is |2c2 / ab|.
14. Area of the parallelogram formed by the lines
a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, a1x + b1y + d1 = 0 and a2x + b2y + d2 = 0 is
|(d1 – c1) (d2 – c2 / a1b2 – a2b1|.
15. (a) Foot of the perpendicular from (a, b) on x – y = 0 is
(a + b / 2, a + b / 2).
(b) Foot of the perpendicular from (a,b) on x + y = 0 is
(a – b / 2, a – b / 2).
16. The image of the line a1x + b1y + c1 = 0 about the line ax + by + c = 0 is .
2(aa1 + bb1) (ax + by + c) =(a2+ b2) (a1x + b1y + c1).
17. Given two vertices (x1, y1) and (x2, y2) of an equilateral MBC, then its third vertex is given by.
[x1 + x2 ± √3 (y1 – y2) / 2, y1 + y2 ∓ √3 (x1 – x2) / 2]
18. The equation of the straight line which passes through a given point (x1, y1) and makes an angle α with the given straight line y = mx + c are
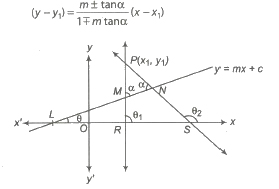
19. The equation of the family of lines passing through the intersection of the lines a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0 is
(a1x + b1y+ c1) + l(a2x + b2y + c2) = 0
where, λ is any real number.
20. Line ax + by + c = 0 divides the line joining the points (x1, y1) and (x2, y2) in the ratio λ : 1, then λ = – (a1x + b1y+ c / a2x + b2y + c).
If λ is positive it divides internally and if λ. is negative, then it divides externally.
21. Area of a polygon of n-sides with vertices A1(x1, y1), A2 (x2, y2) ,… ,An(xn, yn)

22. Equation of the pair of lines through (α, β) and perpendicular to the pair of lines ax2 + 2hxy + by2 = 0 is b (x – α}2 – 2h (x – α)(y – β) + a (y – β)2= 0.