CBSE Class 12 Chemistry
Quick Revision Notes
Chapter 9
- A coordination compound contains a central metal atom or ion surrounded by number of oppositely charged ions or neutral molecules. These ions or molecules re bonded to the metal atom or ion by a coordinate bond.
- Example: K4 [.Fe(CiV)6]
- They do not dissociate into simple ions when dissolved in water.
- When two salts in stoichiometric ratio are crystallised together from their saturated solution they are called double salts
- Example: FeSO4. (NH4) 2SO4.6H20 (Mohr’s salt)
- They dissociate into simple ions when dissolved in water.
- A coordination entity constitutes a central metal atom or ion bonded to a fixed number of ions or molecules.
- Example: In K4 [Fe(CN)6], [.Fe(CiV)6]4-– represents coordination entity.
- In a coordination entity, the atom/ion to which a fixed number of ions/groups are bound
in a definite geometrical arrangement around it, is called the central atom or ion.
+
- Example: In i£4[Fe(CiV)6, Fe is the central metal ion.
- A molecule, ion or group that is bonded to the metal atom or ion in a complex or coordination compound by a coordinate bond is called ligand.
- It may be neutral, positively or negatively charged.
- Examples: H2O, CN~, iVO+etc.
- An atom of the ligand attached directly to the metal is called the donor atom.
- Example: In the complex F4 [.Fe(CiV)6] ,CN is a donor atom.
- The coordination number (CN) of a metal ion in a complex can be defined as the number of ligand donor atoms to which the metal is directly bonded.
- Example: In the complex F4 [Fe(CiV)6], the coordination number of Fe is 6.
- The central atom/ion and the ligands attached to it are enclosed in square bracket and are collectively termed as the coordination sphere.
- Example: In the complex F4 [Fe(CiV)6], [Fe(CiV)6]4_is the coordination sphere.
- The ions present outside the coordination sphere are called counter ions.
- Example: In the complex FjfFe(CiV)6, K+ is the counter ion.
- The spatial arrangement of the ligand atoms which are directly attached to the central atom/ ion defines a coordination polyhedron about the central atom.
- The most common coordination polyhedra are octahedral, square planar and tetrahedral.
- Examples: [PtCZ4]2_is square planar, Fz(CO)4 is tetrahedral while [Cu(NH3)6]3+ is octahedral.
- Charge on the complex ion: The charge on the complex ion is equal to the algebraic sum of the charges on all the ligands coordinated to the central metal ion.
- Denticity: The number of ligating (linking) atoms present in ligand is called denticity.
- The ligands whose only one donor atom is bonded to metal atom are called unidentate ligands.
- Examples: H2O, NH3, CO, CN~
- The ligands which contain two donor atoms or ions through which they are bonded to the metal ion.
- Examples: Ethylene diamine (H2NCH2CH2NH2) has two nitrogen atoms, oxalate ion has two oxygen atoms which can bind with the metal atom.
- When several donor atoms are present in a single ligand, the ligand is called polydentate ligand.
- Examples: In N{CH2CH2NH2)3, the ligand is said to be polydentate and Ethylenediaminetetraacetate ion {EDTA^ ) is an important hexadentate ligand. It can bind through two nitrogen and four oxygen atoms to a central metal ion.
- An inorganic metal complex in which there is a close ring of atoms caused by attachment of a ligand to a metal atom at two points.
- An example is the complex ion formed between ethylene diamine and cupric ion,
.
- Ligands which can ligate (link) through two different atoms present in it are called ambidentate ligand.
- Example: N02~ and SCN~ . Here, N0^~ can link through N as well as O while SCN~ can link through S as well as N atom.
- Werner was able to explain the nature of bonding in complexes.
- The postulates of Werner’s theory are:
- . Metal shows two different kinds of valencies: primary valence and secondary valence.
- . The ions/ groups bound by secondary linkages to the metal have characteristic spatial arrangements corresponding to different coordination numbers.
- . The most common geometrical shapes in coordination compounds are octahedral, square planar and tetrahedral.
- This valence is normally ionisable.
- It is equal to positive charge on central metal atom.
- These valencies are satisfied by negatively charged ions.
- Example: In CrCl$, the primary valency is three. It is equal to oxidation state of central metal ion.
- This valence is non – ionisable.
- The secondary valency equals the number of ligand atoms coordinated to the metal. It is also called coordination number of the metal.
- It is commonly satisfied by neutral and negatively charged, sometimes by positively charged ligands.
- Oxidation number of central atom: The oxidation number of the central atom in a complex is defined as the charge it would carry if all the ligands are removed along with the electron pairs that are shared with the central atom.
- Homoleptic complexes: Those complexes in which metal or ion is coordinate bonded
Q I
to only one kind of donor atoms. For example:
- Heteroleptic complexes: Those complexes in which metal or ion is coordinate bonded to more than one kind of donor atoms. For example:
- Isomers: Two or more compounds which have same chemical formula but different arrangement of atoms are called isomers.
- Types of isomerism:
- . Linkage isomerism
- . Solvate isomerism or hydrate isomerism
- . Ionisation isomerism
- . Coordination isomerism
- Structural isomerism
- Stereoisomerism
- . Geometrical isomerism
- . Optical isomerism
- It arises due to the difference in structures of coordination compounds.
- Structural isomerism, or constitutional isomerism, is a form of isomerism in which molecules with the same molecular formula have atoms bonded together in different orders.
- It arises when the counter ion in a complex salt is itself a potential ligand and can displace a ligand which can then become the counter ion.
- Example:
- It is isomerism in which solvent is involved as ligand.
- If solvent is water it is called hydrate isomerism, e.g., [Cr(H20)§\ Clz and [CrCl2(H2O)4] Cl2. 2H2O.
- It arises in a coordination compound containing ambidentate ligand.
- In the isomerism, a ligand can form linkage with metal through different atoms.
- Example: and .
- This type of isomerism arises from the interchange of ligands between cationic and anionic entities of different metal ions present in a complex.
- Example: [Co(AT-Hs)6] [Cr(C2O4)3] and .
- Stereoisomerism: This type of isomerism arises because of different spatial arrangement.
- Geometrical isomerism: It arises in heteroleptic complexes due to different possible geometrical arrangements of ligands.
- Optical isomerism: Optical isomers are those isomers which are non-superimposable mirror images.
- Valence bond theory:
- According to this theory, the metal atom or ion under the influence of ligands can use its (n-1)d, ns, np or ns, np, nd orbitals for hybridisation to yield a set of equivalent orbitals of definite geometry such as octahedral, tetrahedral, and square planar.
- These hybridised orbitals are allowed to overlap with ligand orbitals that can donate electron pairs for bonding.
|
Coordination Number |
Type of hybridisation |
Shape of hybrid |
|
4 |
sp3 |
Tetrahedral |
|
4 |
dsp1 |
Square planar |
|
5 |
sjPd |
Trigonalbipyramidal |
|
6 |
SjPd2 (nd orbitals are involved – outer orbital complex or high spin or spin free complex) |
Octahedral |
|
6 |
d2sjP {n — 1) d orbitals are involved -inner orbital or low spin or spin paired complex) |
Octahedral |
• Magnetic properties of coordination compounds:
A coordination compound is paramagnetic in nature if it has unpaired electrons and diamagnetic if all the electrons in the coordination compound are paired.
Magnetic moment M = ^n(n + 2) where n is number of unpaired electrons.
- It assumes the ligands to be point charges and there is electrostatic force of attraction between ligands and metal atom or ion.
- It is theoretical assumption.
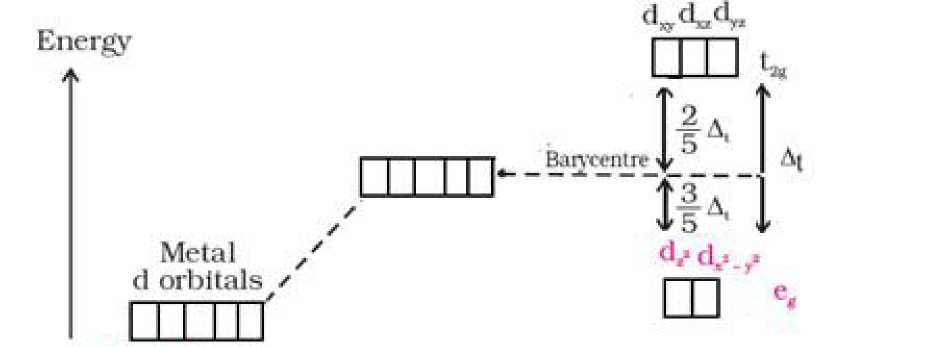
• Crystal field splitting in octahedral coordination complexes:

(I=.*1 tlr’ dwdMdp Awerageeftefgy SpHtttngofdorbttato
ofihe dorbUaL$ In in octahedral Frec metal ion spherical crystal HHd crystal flelcJ
• For the same metal, the same ligands and metal-ligand distances, the difference in
energy between eg and t2g level is

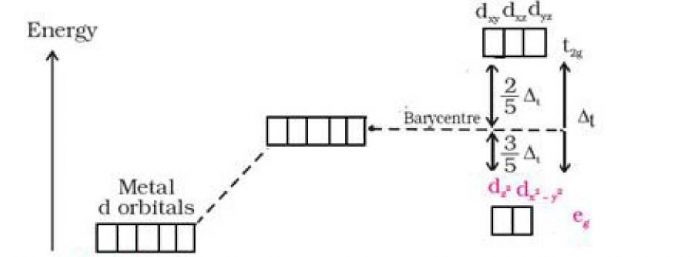
Crystal field splitting in tetrahedral coordination complexes:
cl v d/ ^ d„ cKi Average eEiergy Spllttttig <>f d orbitals
of Ihe d orbitals jn |u tetrahedral Free metal ion spherricaJ crystal HeIcI ory$taJ field
- Metal carbonyls are homoleptic complexes in which carbon monoxide (CO) acts as the ligand.
- Example: Ni(CO)4
- The metal-carbon bond in metal carbonyls possess both s and p character.
- The M-C cr bond is formed by the donation of lone pair of electrons from the carbonyl carbon into a vacant orbital of the metal.
- The M-C 7rbond is formed by the donation of a pair of electrons from a filled d orbital of metal into the vacant antibonding^* orbital of carbon monoxide.
- The metal to ligand bonding creates a synergic effect which strengthens the bond between CO and the metal.