NCERT Exemplar Problems Class 12 Mathematics Chapter 9 Differential Equations
Short Answer Type Questions

2. Find the differential equation of all non-vertical lines in a plane.







13. Form the differential equation having y = (sin-1 x)2+ A cos-1 x + B, where A and B are arbitrary constants, as its general solution.
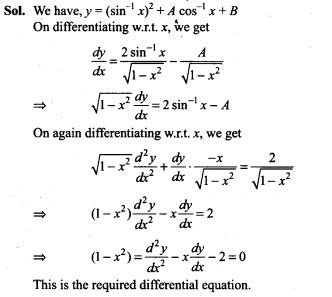
14. Form the differential equation* of all circles which pass through origin and whose centres lie on y-axis.



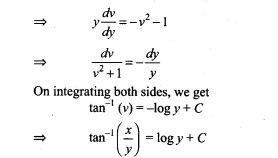
19. Solve : (x + y)(dx -dy) = dx + dy
[Hint: Substitute x+y = z after separating dx and dy]

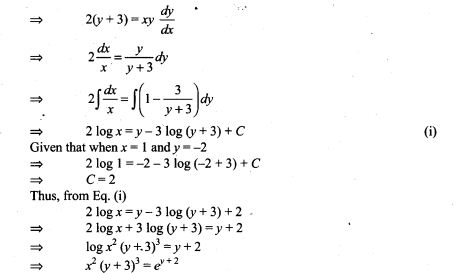
21. Solve the differential equation dy = cos x (2 – y cosec x) dx given that y=2 when x = π /2.

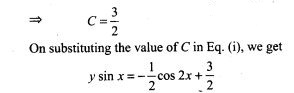
22. Form the differential equation by eliminating A and B in Ax2 -By2 = 1.
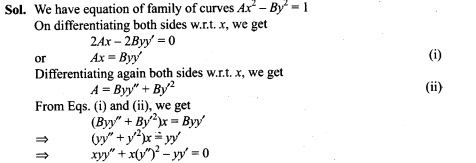
23. Solve the differential equation (1 +y2) tan-1 x dx + 2y (1+x2)dy=0.
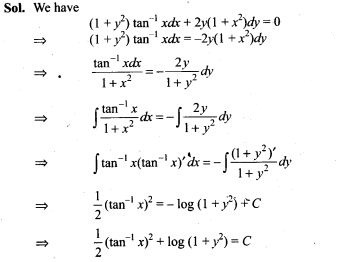
24. Find the differential equation of system of concentric circles with centre (1,2).
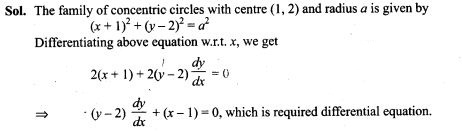
Long Answer Type Questions




31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abscissa and ordinate of the point.

32. Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.

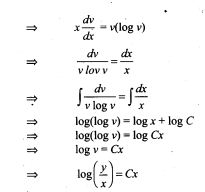
Objective Type Questions







60. Family y = Ax + A3 of curves will correspond to a differential equation of order ,
(a) 3 (b) 2 (c) 1 (d) not defined
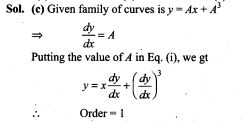
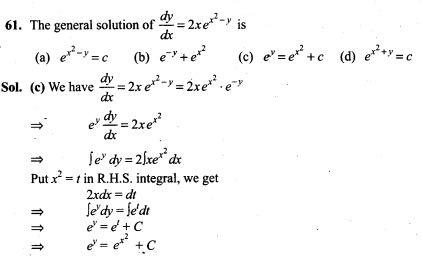
62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is
(a) an ellipse (b) parabola
(c) circle (d) rectangular hyperbola






Fill in the Blanks Type Questions




True/False Type Questions



