Contents
- Question 1:
- Question 2:
- Question 3:
- Question 4:
- Question 5:
- Question 6:
- Question 7:
- Question 8:
- Question 9:
- Question 10:
- Question 11:
- Question 12:
- Question 13:
- Question 14:
- Question 15:
- Question 1:
- Question 2:
- Question 3:
- Question 4:
- Question 5:
- Question 6:
- Question 7:
- Question 8:
- Question 9:
- Question 10:
- Question 11:
- Question 12:
- Question 13:
- Question 14:
- Question 15:
- Question 1:
- Question 2:
- Question 3:
- Question 4:
- Question 5:
- Question 6:
- Question 7:
- Question 8:
- Question 9:
- Question 10:
- Question 11:
- Question 12:
- Question 13:
- Question 14:
- Question 15:
- Question 16:
- Question 17:
- Question 1:
- Question 2:
- Question 3:
- Question 4:
- Question 5:
- Question 6:
- Question 7:
- Question 8:
- Question 9:
- Question 10:
- Question 11:
- Question 12:
- Question 13:
- Question 14:
- Question 15:
- Question 16:
- Question 17:
- Question 18:
- Question 19:
- Question 20:
- Question 21:
- Question 22:
- Question 23:
- Question 24:
- Question 25:
- Question 26:
Angles, Linesand Triangles
Question 1:
Exercise 4A
- Angle: Two rays having a common end point form an angle.
- Interior of an angle: The interior of ∠AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
- Obtuse angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.
- Reflex angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle.
- Complementary angles: Two angles are said to be complementary, if the sum of their measures is 90o.
- Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°.
Question 2:
∠A = 36° 27′ 46″ and ∠B = 28° 43′ 39″
∴ Their sum = (36° 27′ 46″) + (28° 43′ 39″)

Therefore, the sum ∠A + ∠B = 65° 11′ 25″
Question 3:
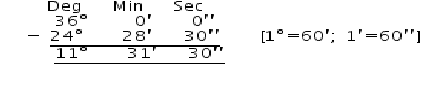
Let ∠A = 36° and ∠B = 24° 28′ 30″ Their difference = 36° – 24° 28′ 30″
Thus the difference between two angles is ∠A – ∠B = 11° 31′ 30″
Question 4:
-
- Complement of 58o = 90o – 58o = 32o
- Complement of 16o = 90 – 16o = 74o
-
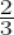
of a right angle =
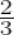
× 90o = 60o Complement of 60o = 90o – 60o = 30o - 1o = 60′
⇒ 90o = 89o 60′
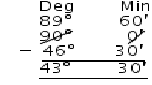
Complement of 46o 30′ = 90o – 46o 30′ = 43o 30′ (v) 90o = 89o 59′ 60″
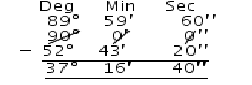
Complement of 52o 43′ 20″ = 90o – 52o 43′ 20″
= 37o 16′ 40″
(vi) 90o = 89o 59′ 60″

∴ Complement of (68o 35′ 45″)
= 90o – (68o 35′ 45″)
= 89o 59′ 60″ – (68o 35′ 45″)
= 21o 24′ 15″
Question 5:
- Supplement of 63o = 180o – 63o = 117o
- Supplement of 138o = 180o – 138o = 42o
-
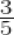
of a right angle =
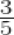
× 90o = 54o
∴ Supplement of 54o = 180o – 54o = 126o
- 1o = 60′
⇒ 180o = 179o 60′
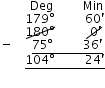
Supplement of 75o 36′ = 180o – 75o 36′ = 104o 24′ (v) 1o = 60′, 1′ = 60″
⇒ 180o = 179o 59′ 60″
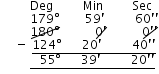
Supplement of 124o 20′ 40″ = 180o – 124o 20′ 40″
= 55o 39′ 20″
(vi) 1o = 60′, 1′ = 60″
⇒ 180o = 179o 59′ 60″

∴ Supplement of 108o 48′ 32″ = 180o – 108o 48′ 32″
= 71o 11′ 28″.
Question 6:
-
-

Let the required angle be xo Then, its complement = 90o – xo
-
∴ The measure of an angle which is equal to its complement is 45o.
-
-

Let the required angle be xo Then, its supplement = 180o – xo
-
∴ The measure of an angle which is equal to its supplement is 90o.
Question 7:
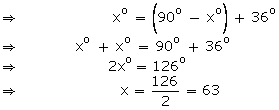
Let the required angle be xo Then its complement is 90o – xo
∴ The measure of an angle which is 36o more than its complement is 63o.
Question 8:

Let the required angle be xo Then its supplement is 180o – xo
![]()
∴ The measure of an angle which is 25o less than its supplement is
Question 9:

Let the required angle be xo Then, its complement = 90o – xo
∴ The required angle is 72o.
Question 10:

Let the required angle be xo Then, its supplement is 180o – xo
∴ The required angle is 150o.
Question 11:
Let the required angle be xo
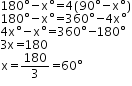
Then, its complement is 90o – xo and its supplement is 180o – xo That is we have,
∴ The required angle is 60o.
Question 12:
Let the required angle be xo

Then, its complement is 90o – xo and its supplement is 180o – xo
∴ The required angle is 45o.
Question 13:
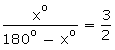
Let the two required angles be xo and 180o – xo. Then,
⇒ 2x = 3(180 – x)
⇒ 2x = 540 – 3x
⇒ 3x + 2x = 540
⇒ 5x = 540
⇒ x = 108
Thus, the required angles are 108o and 180o – xo = 180 o – 108o = 72o.
Question 14:
![]()
Let the two required angles be xo and 90o – xo. Then
⇒ 5x = 4(90 – x)
⇒ 5x = 360 – 4x
⇒ 5x + 4x = 360
⇒ 9x = 360
⇒ x =
![]()
= 40
Thus, the required angles are 40o and 90o – xo = 90 o – 40o = 50o.
Question 15:
Let the required angle be xo.
Then, its complementary and supplementary angles are (90o – x) and (180o – x) respectively.
Then, 7(90o – x) = 3 (180o – x) – 10o
⇒ 630o – 7x = 540o – 3x – 10o
⇒ 7x – 3x = 630o – 530o
⇒ 4x = 100o
⇒ x = 25o
Thus, the required angle is 25o.
Question 1:
Exercise 4B
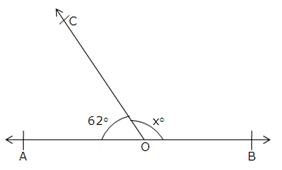
Since ∠BOC and ∠COA form a linear pair of angles, we have
∠BOC + ∠COA = 180o
⇒ xo + 62o = 180o
⇒ x = 180 – 62
∴ x = 118o
Question 2:
Since, ∠BOD and ∠DOA form a linear pair.
∠BOD + ∠DOA = 180o
∴ ∠BOD + ∠DOC + ∠COA = 180o
⇒ (x + 20)o + 55o + (3x – 5)o = 180o
⇒ x + 20 + 55 + 3x – 5 = 180
⇒ 4x + 70 = 180
⇒ 4x = 180 – 70 = 110
⇒ x =
![]()
= 27.5
∴ ∠AOC = (3 × 27.5 – 5)o = 82.5-5 = 77.5o And, ∠BOD = (x + 20)o = 27.5o + 20o = 47.5o.
Question 3:
Since ∠BOD and ∠DOA from a linear pair of angles.
⇒ ∠BOD + ∠DOA = 180o
⇒ ∠BOD + ∠DOC + ∠COA = 180o
⇒ xo + (2x – 19)o + (3x + 7)o = 180o
⇒ 6x – 12 = 180
⇒ 6x = 180 + 12 = 192
⇒ x =
![]()
= 32
⇒ x = 32
⇒ ∠AOC = (3x + 7)o = (3 32 + 7)o = 103o
⇒ ∠COD = (2x – 19)o = (2 32 – 19)o = 45o
and ∠BOD = xo = 32o
Question 4:
x: y: z = 5: 4: 6
The sum of their ratios = 5 + 4 + 6 = 15 But x + y + z = 180o
[Since, XOY is a straight line]
So, if the total sum of the measures is 15, then the measure of x is 5. If the sum of angles is 180o, then, measure of x =
![]()
× 180 = 60
And, if the total sum of the measures is 15, then the measure of y is 4. If the sum of the angles is 180o, then, measure of y =
![]()
× 180 = 48 And ∠z = 180o – ∠x – ∠y
= 180o – 60o – 48o
= 180o – 108o = 72o
∴ x = 60, y = 48 and z = 72.
Question 5:
AOB will be a straight line, if two adjacent angles form a linear pair.
∴ ∠BOC + ∠AOC = 180o
⇒ (4x – 36)o + (3x + 20)o = 180o
⇒ 4x – 36 + 3x + 20 = 180
⇒ 7x – 16 = 180o
⇒ 7x = 180 + 16 = 196
⇒ x =
![]()
= 28
∴ The value of x = 28.
Question 6:
Since ∠AOC and ∠AOD form a linear pair.
∴ ∠AOC + ∠AOD = 180o
⇒ 50o + ∠AOD = 180o
⇒ ∠AOD = 180o – 50o = 130o
∠AOD and ∠BOC are vertically opposite angles.
∠AOD = ∠BOC
⇒ ∠BOC = 130o
∠BOD and ∠AOC are vertically opposite angles.
∴ ∠BOD = ∠AOC
⇒ ∠BOD = 50o
Question 7:
Since ∠COE and ∠DOF are vertically opposite angles, we have,
∠COE = ∠DOF
⇒ ∠z = 50o
Also ∠BOD and ∠COA are vertically opposite angles. So, ∠BOD = ∠COA
⇒ ∠t = 90o
As ∠COA and ∠AOD form a linear pair,
∠COA + ∠AOD = 180o
⇒ ∠COA + ∠AOF + ∠FOD = 180o [∠t = 90o]
⇒ t + x + 50o = 180o
⇒ 90o + xo + 50o = 180o
⇒ x + 140 = 180
⇒ x = 180 – 140 = 40
Since ∠EOB and ∠AOF are vertically opposite angles So, ∠EOB = ∠AOF
⇒ y = x = 40
Thus, x = 40 = y = 40, z = 50 and t = 90
Question 8:
Since ∠COE and ∠EOD form a linear pair of angles.
⇒ ∠COE + ∠EOD = 180o
⇒ ∠COE + ∠EOA + ∠AOD = 180o
⇒ 5x + ∠EOA + 2x = 180
⇒ 5x + ∠BOF + 2x = 180
[∴ ∠EOA and BOF are vertically opposite angles so, ∠EOA = ∠BOF]
⇒ 5x + 3x + 2x = 180
⇒ 10x = 180
⇒ x = 18
Now ∠AOD = 2xo = 2 × 18o = 36o
∠COE = 5xo = 5 × 18o = 90o
and, ∠EOA = ∠BOF = 3xo = 3 × 18o = 54o
Question 9:
Let the two adjacent angles be 5x and 4x. Now, since these angles form a linear pair. So, 5x + 4x = 180o
⇒ 9x = 180o
⇒ x =
![]()
= 20
∴ The required angles are 5x = 5x = 5 20o = 100o and 4x = 4 × 20o = 80o
Question 10:
Let two straight lines AB and CD intersect at O and let ∠AOC = 90o.
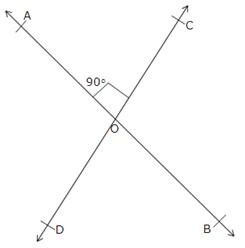
Now, ∠AOC = ∠BOD [Vertically opposite angles]
⇒ ∠BOD = 90o
Also, as ∠AOC and ∠AOD form a linear pair.
⇒ 90o + ∠AOD = 180o
⇒ ∠AOD = 180o – 90o = 90o
Since, ∠BOC = ∠AOD [Verticallty opposite angles]
⇒ ∠BOC = 90o
Thus, each of the remaining angles is 90o.
Question 11:
Since, ∠AOD and ∠BOC are vertically opposite angles.
∴ ∠AOD = ∠BOC
Now, ∠AOD + ∠BOC = 280o [Given]
⇒ ∠AOD + ∠AOD = 280o
⇒ 2∠AOD = 280o
⇒ ∠AOD =
![]()
= 140o
⇒ ∠BOC = ∠AOD = 140o
As, ∠AOC and ∠AOD form a linear pair. So, ∠AOC + ∠AOD = 180o
⇒ ∠AOC + 140o = 180o
⇒ ∠AOC = 180o – 140o = 40o
Since, ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠AOC = ∠BOD
⇒ ∠BOD = 40o
∴ ∠BOC = 140o, ∠AOC = 40o , ∠AOD = 140o and ∠BOD = 40o.
Question 12:
Since ∠COB and ∠BOD form a linear pair So, ∠COB + ∠BOD = 180o
⇒ ∠BOD = 180o – ∠COB …. (1)
Also, as ∠COA and ∠AOD form a linear pair. So, ∠COA + ∠AOD = 180o
⇒ ∠AOD = 180o – ∠COA
⇒ ∠AOD = 180o – ∠COB …. (2)
[Since, OC is the bisector of ∠AOB, ∠BOC = ∠AOC] From (1) and (2), we get,
∠AOD = ∠BOD (Proved)
 Question 13:
Question 13:
Let QS be a perpendicular to AB. Now, ∠PQS = ∠SQR
Because angle of incident = angle of reflection
⇒ ∠PQS = ∠SQR =
![]()
= 56o
Since QS is perpendicular to AB, ∠PQA and ∠PQS are complementary angles. Thus, ∠PQA + ∠PQS = 90o
⇒ ∠PQA + 56o = 90o
⇒ ∠PQA = 90o – 56o = 34o
Question 14:
Given : AB and CD are two lines which are intersecting at O. OE is a ray bisecting the
∠BOD. OF is a ray opposite to ray OE.

To Prove: ∠AOF = ∠COF
Proof : Since
![]()
and
![]()
are two opposite rays,
![]()
is a straight line passing through O.
∴ ∠AOF = ∠BOE and ∠COF = ∠DOE
[Vertically opposite angles] But ∠BOE = ∠DOE (Given)
∴ ∠AOF = ∠COF
Hence, proved.
Question 15:
Given:
![]()
is the bisector of ∠BCD and
![]()
is the bisector of ∠ACD. To Prove: ∠ECF = 90o
Proof: Since ∠ACD and ∠BCD forms a linear pair.
∠ACD + ∠BCD = 180o
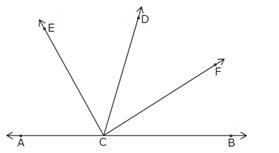
∠ACE + ∠ECD + ∠DCF + ∠FCB = 180o
∠ECD + ∠ECD + ∠DCF + ∠DCF = 180o
because ∠ACE = ∠ECD and ∠DCF = ∠FCB
2(∠ECD) + 2 (∠CDF) = 180o
2(∠ECD + ∠DCF) = 180o
∠ECD + ∠DCF =
![]()
= 90o
∠ECF = 90o (Proved)
Question 1:
Exercise 4C
Since AB and CD are given to be parallel lines and t is a transversal. So, ∠5 = ∠1 = 70o [Corresponding angles are equal]
∠3 = ∠1 = 70o [Vertically opp. Angles]
∠3 + ∠6 = 180o [Co-interior angles on same side]
∴ ∠6 = 180o – ∠3
= 180o – 70o = 110o
∠6 = ∠8 [Vertically opp. Angles]
⇒ ∠8 = 110o
⇒ ∠4 + ∠5 = 180o [Co-interior angles on same side]
∠4 = 180o – 70o = 110o
∠2 = ∠4 = 110o [ Vertically opposite angles]
∠5 = ∠7 [Vertically opposite angles] So, ∠7 = 70o
∴ ∠2 = 110o, ∠3 = 70o , ∠4 = 110o, ∠5 = 70o, ∠6 = 110o, ∠7 = 70o and ∠8 = 110o.
Question 2:
Since ∠2 : ∠1 = 5 : 4.
Let ∠2 and ∠1 be 5x and 4x respectively.
Now, ∠2 + ∠1 = 180o , because ∠2 and ∠1 form a linear pair. So, 5x + 4x = 180o
⇒ 9x = 180o
⇒ x = 20o
∴ ∠1 = 4x = 4 × 20o = 80o And ∠2 = 5x = 5 × 20o = 100o
∠3 = ∠1 = 80o [Vertically opposite angles]
And ∠4 = ∠2 = 100o [Vertically opposite angles]
∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles] So, ∠5 = 80o and ∠6 = 100o
∠8 = ∠6 = 100o [Vertically opposite angles] And ∠7 = ∠5 = 80o [Vertically opposite angles]
Thus, ∠1 = 80o, ∠2 = 100o, ∠3 = ∠80o, ∠4 = 100o, ∠5 = 80o, ∠6 = 100o, ∠7 = 80o and
∠8 = 100o.
Question 3:
Given: AB || CD and AD || BC To Prove: ∠ADC = ∠ABC
Proof: Since AB || CD and AD is a transversal. So sum of consecutive interior angles is
180o.
⇒ ∠BAD + ∠ADC = 180o ….(i)
Also, AD || BC and AB is transversal. So, ∠BAD + ∠ABC = 180o ….(ii) From (i) and (ii) we get:
∠BAD + ∠ADC = ∠BAD + ∠ABC
⇒ ∠ADC = ∠ABC (Proved)
Question 4:
-
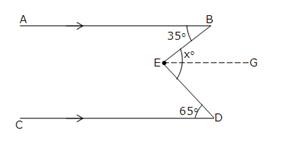
Through E draw EG || CD. Now since EG||CD and ED is a transversal.
So, ∠GED = ∠EDC = 65o [Alternate interior angles] Since EG || CD and AB || CD,
EG||AB and EB is transversal.
So, ∠BEG = ∠ABE = 35o [Alternate interior angles] So, ∠DEB = xo
⇒ ∠BEG + ∠GED = 35o + 65o = 100o.
Hence, x = 100.
-
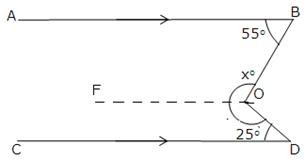
Through O draw OF||CD.
Now since OF || CD and OD is transversal.
∠CDO + ∠FOD = 180o
[sum of consecutive interior angles is 180o]
⇒ 25o + ∠FOD = 180o
⇒ ∠FOD = 180o – 25o = 155o
As OF || CD and AB || CD [Given] Thus, OF || AB and OB is a transversal.
So, ∠ABO + ∠FOB = 180o [sum of consecutive interior angles is 180o]
⇒ 55o + ∠FOB = 180o
⇒ ∠FOB = 180o – 55o = 125o
Now, xo = ∠FOB + ∠FOD = 125o + 155o = 280o.
Hence, x = 280.
-
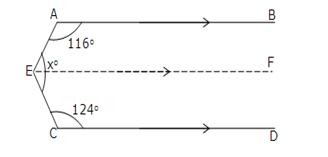
Through E, draw EF || CD.
Now since EF || CD and EC is transversal.
∠FEC + ∠ECD = 180o
[sum of consecutive interior angles is 180o]
⇒ ∠FEC + 124o = 180o
⇒ ∠FEC = 180o – 124o = 56o
Since EF || CD and AB ||CD
So, EF || AB and AE is a trasveral.
So, ∠BAE + ∠FEA = 180o
[sum of consecutive interior angles is 180o]
∴ 116o + ∠FEA = 180o
⇒ ∠FEA = 180o – 116o = 64o
Thus, xo = ∠FEA + ∠FEC
= 64o + 56o = 120o.
Hence, x = 120.
Question 5:
Since AB || CD and BC is a transversal.
So, ∠ABC = ∠BCD [atternate interior angles]
⇒ 70o = xo + ∠ECD ….(i)
Now, CD || EF and CE is transversal.
So, ∠ECD + ∠CEF = 180o
∴ ∠ECD + 130o = 180o
[sum of consecutive interior angles is 180o]
⇒ ∠ECD = 180o – 130o = 50o
Putting ∠ECD = 50o in (i) we get, 70o = xo + 50o
⇒ x = 70 – 50 = 20
Question 6:
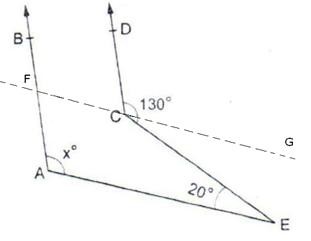
Through C draw FG || AE
Now, since CG || BE and CE is a transversal.
So, ∠GCE = ∠CEA = 20o
∴ ∠DCG = 130o – ∠GCE
= 130o – 20o = 110o
[Alternate angles]
Also, we have AB || CD and FG is a transversal.
So, ∠BFC = ∠DCG = 110o
As, FG || AE, AF is a transversal.
[Corresponding angles]
∠BFG = ∠FAE [Corresponding angles]
∴ xo = ∠FAE = 110o. Hence, x = 110
Question 7:
Given: AB || CD
To Prove: ∠BAE – ∠DCE = ∠AEC
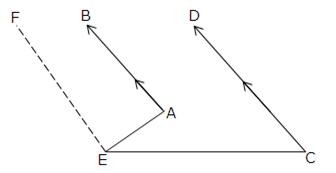
Construction : Through E draw EF || AB Proof : Since EF || AB, AE is a transversal. So, ∠BAE + ∠AEF = 180O ….(i)
[sum of consecutive interior angles is 180o] As EF || AB and AB || CD [Given]
So, EF || CD and EC is a transversal.
So, ∠FEC + ∠DCE = 180o ….(ii)
[sum of consecutive interior angles is 180o] From (i) and (ii) we get,
∠BAE + ∠AEF = ∠FEC + ∠DCE
⇒ ∠BAE – ∠DCE = ∠FEC – ∠AEF = ∠AEC [Proved]
Question 8:
Since AB || CD and BC is a transversal.
So, ∠BCD = ∠ABC = xo
[Alternate angles]
As BC || ED and CD is a transversal.
∠BCD + ∠EDC = 180o
⇒ ∠BCD + 75o =180o
⇒ ∠BCD = 180o – 75o = 105o
∠ABC = 105o
∴ xo = ∠ABC = 105o Hence, x = 105.
[since ∠BCD = ∠ABC]
Question 9:
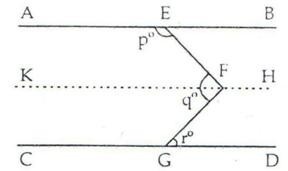
Through F, draw KH || AB || CD
Now, KF || CD and FG is a transversal.
⇒ ∠KFG = ∠FGD = ro …. (i) [alternate angles]
Again AE || KF, and EF is a transversal.
So, ∠AEF + ∠KFE = 180o
∠KFE = 180o – po …. (ii) Adding (i) and (ii) we get,
∠KFG + ∠KFE = 180 – p + r
⇒ ∠EFG = 180 – p + r
⇒ q = 180 – p + r i.e., p + q – r = 180
 Question 10:
Question 10:
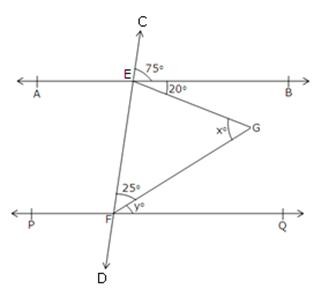
Since AB || PQ and EF is a transversal.
So, ∠CEB = ∠EFQ [Corresponding angles]
⇒ ∠EFQ = 75o
⇒ ∠EFG + ∠GFQ = 75o
⇒ 25o + yo = 75o
⇒ y = 75 – 25 = 50
Also, ∠BEF + ∠EFQ = 180o
∠BEF = 180o – ∠EFQ
= 180o – 75o
∠BEF = 105o
[sum of consecutive interior angles is 180o]
∴ ∠FEG + ∠GEB = ∠BEF = 105o
⇒ ∠FEG = 105o – ∠GEB = 105o – 20o = 85o
In ∆EFG we have,
xo + 25o + ∠FEG = 180o
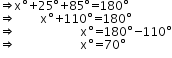
Hence, x = 70.
Question 11:
Since AB || CD and AC is a transversal.
So, ∠BAC + ∠ACD = 180o
⇒ ∠ACD = 180o – ∠BAC
= 180o – 75o = 105o
[sum of consecutive interior angles is 180o]
⇒ ∠ECF = ∠ACD [Vertically opposite angles]
∠ECF = 105o
Now in ∆CEF,
∠ECF + ∠CEF + ∠EFC =180o
⇒ 105o + xo + 30o = 180o
⇒ x = 180 – 30 – 105 = 45
Hence, x = 45.
Question 12:
Since AB || CD and PQ a transversal.
So, ∠PEF = ∠EGH [Corresponding angles]
⇒ ∠EGH = 85o
∠EGH and ∠QGH form a linear pair. So, ∠EGH + ∠QGH = 180o
⇒ ∠QGH = 180o – 85o = 95o
Similarly, ∠GHQ + 115o = 180o
⇒ ∠GHQ = 180o – 115o = 65o
In ∆GHQ, we have, xo + 65o + 95o = 180o
⇒ x = 180 – 65 – 95 = 180 – 160
∴ x = 20
 Question 13:
Question 13:
Since AB || CD and BC is a transversal. So, ∠ABC = ∠BCD
⇒ x = 35
Also, AB || CD and AD is a transversal. So, ∠BAD = ∠ADC
⇒ z = 75
In ∆ABO, we have,
∠AOB + ∠BAO + ∠BOA = 180o
⇒ xo + 75o + yo = 180o
⇒ 35 + 75 + y = 180
⇒ y = 180 – 110 = 70
∴ x = 35, y = 70 and z = 75.
 Question 14:
Question 14:
Since AB || CD and PQ is a transversal. So, y = 75 [Alternate angle]
Since PQ is a transversal and AB || CD, so x + APQ = 180o
[Sum of consecutive interior angles]
⇒ xo = 180o – APQ
⇒ x = 180 – 75 = 105
Also, AB || CD and PR is a transversal.
So, ∠APR = ∠PRD [Alternate angle]
⇒ ∠APQ + ∠QPR = ∠PRD [Since ∠APR = ∠APQ + ∠QPR]
⇒ 75o + zo = 125o
⇒ z = 125 – 75 = 50
∴ x = 105, y = 75 and z = 50.
Question 15:
∠PRQ = xo = 60o
[vertically opposite angles]
Since EF || GH, and RQ is a transversal. So, ∠x = ∠y [Alternate angles]
⇒ y = 60
AB || CD and PR is a transversal.
So, ∠PRD = ∠APR [Alternate angles]
⇒ ∠PRQ + ∠QRD = ∠APR [since ∠PRD = ∠PRQ + ∠QRD]
⇒ x + ∠QRD = 110o
⇒ ∠QRD = 110o – 60o = 50o
In ∆QRS, we have,
∠QRD + to + yo = 180o
⇒ 50 + t + 60 = 180
⇒ t = 180 – 110 = 70
Since, AB || CD and GH is a transversal So, zo = to = 70o [Alternate angles]
∴ x = 60 , y = 60, z = 70 and t = 70
Question 16:
- Lines l and m will be parallel if 3x – 20 = 2x + 10
[Since, if corresponding angles are equal, lines are parallel]
⇒ 3x – 2x = 10 + 20
⇒ x = 30
- Lines will be parallel if (3x + 5)o + 4xo = 180o
[if sum of pairs of consecutive interior angles is 180o, the lines are parallel] So, (3x + 5) + 4x = 180
⇒ 3x + 5 + 4x = 180
⇒ 7x = 180 – 5 = 175
⇒ x =
![]()
= 25
Question 17:
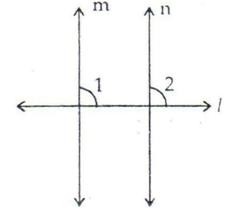
Given: Two lines m and n are perpendicular to a given line l.
To Prove: m || n Proof : Since m ⊥ l So, ∠1 = 90o Again, since n ⊥ l
∠2 = 90o
∴ ∠1 = ∠2 = 90o
But ∠1 and ∠2 are the corresponding angles made by the transversal l with lines m and n and they are proved to be equal.
Thus, m || n.
Question 1:
Exercise 4D
Since, sum of the angles of a triangle is 180o
∠A + ∠B + ∠C = 180o
⇒ ∠A + 76o + 48o = 180o
⇒ ∠A = 180o – 124o = 56o
∴ ∠A = 56o
Question 2:
Let the measures of the angles of a triangle are (2x)o, (3x)o and (4x)o. Then, 2x + 3x + 4x = 180 [sum of the angles of a triangle is 180o ]
⇒ 9x = 180
⇒ x =
![]()
= 20
∴ The measures of the required angles are: 2x = (2 × 20)o = 40o
3x = (3 × 20)o = 60o
4x = (4 × 20)o = 80o
Question 3:
Let 3∠A = 4∠B = 6∠C = x (say) Then, 3∠A = x
⇒ ∠A =
![]()
4∠B = x
⇒ ∠B =
![]()
and 6∠C = x
⇒ ∠C =
![]()
As ∠A + ∠B + ∠C = 180o
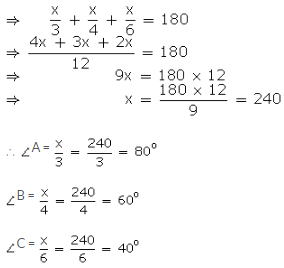
Question 4:
∠A + ∠B = 108o [Given]
But as ∠A, ∠B and ∠C are the angles of a triangle,
∠A + ∠B + ∠C = 180o
⇒ 108o + ∠C = 180o
⇒ C = 180o – 108o = 72o
Also, ∠B + ∠C = 130o [Given]
⇒ ∠B + 72o = 130o
⇒ ∠B = 130o – 72o = 58o Now as, ∠A + ∠B = 108o
⇒ ∠A + 58o = 108o
⇒ ∠A = 108o – 58o = 50o
∴ ∠A = 50o, ∠B = 58o and ∠C = 72o.
Question 5:
Since. ∠A , ∠B and ∠C are the angles of a triangle . So, ∠A + ∠B + ∠C = 180o
Now, ∠A + ∠B = 125o [Given]
∴ 125o + ∠C = 180o
⇒ ∠C = 180o – 125o = 55o
Also, ∠A + ∠C = 113o [Given]
⇒ ∠A + 55o = 113o
⇒ ∠A = 113o – 55o = 58o Now as ∠A + ∠B = 125o
⇒ 58o + ∠B = 125o
⇒ ∠B = 125o – 58o = 67o
∴ ∠A = 58o, ∠B = 67o and ∠C = 55o.
Question 6:
Since, ∠P, ∠Q and ∠R are the angles of a triangle. So, ∠P + ∠Q + ∠R = 180o ….(i)
Now, ∠P – ∠Q = 42o [Given]
⇒ ∠P = 42o + ∠Q ….(ii)
and ∠Q – ∠R = 21o [Given]
⇒ ∠R = ∠Q – 21o ….(iii)
Substituting the value of ∠P and ∠R from (ii) and (iii) in (i), we get,
⇒ 42o + ∠Q + ∠Q + ∠Q – 21o = 180o
⇒ 3∠Q + 21o = 180o
⇒ 3∠Q = 180o – 21o = 159o
∠Q =
![]()
= 53o
∴ ∠P = 42o + ∠Q
= 42o + 53o = 95o
∠R = ∠Q – 21o
= 53o – 21o = 32o
∴ ∠P = 95o, ∠Q = 53o and ∠R = 32o.
Question 7:
Given that the sum of the angles A and B of a ABC is 116o, i.e., ∠A + ∠B = 116o. Since, ∠A + ∠B + ∠C = 180o
So, 116o + ∠C = 180o
⇒ ∠C = 180o – 116o = 64o
Also, it is given that:
∠A – ∠B = 24o
⇒ ∠A = 24o + ∠B
Putting, ∠A = 24o + ∠B in ∠A + ∠B = 116o, we get,
⇒ 24o + ∠B + ∠B = 116o
⇒ 2∠B + 24o = 116o
⇒ 2∠B = 116o – 24o = 92o
∠B =
![]()
= 46o
Therefore, ∠A = 24o + 46o = 70o
∴ ∠A = 70o, ∠B = 46o and ∠C = 64o.
Question 8:
Let the two equal angles, A and B, of the triangle be xo each. We know,
∠A + ∠B + ∠C = 180o
⇒ xo + xo + ∠C = 180o
⇒ 2xo + ∠C = 180o ….(i) Also, it is given that,
∠C = xo + 18o ….(ii)
Substituting ∠C from (ii) in (i), we get,
⇒ 2xo + xo + 18o = 180o
⇒ 3xo = 180o – 18o = 162o x =
![]()
= 54o
Thus, the required angles of the triangle are 54o, 54o and xo + 18o = 54o + 18o = 72o.
Question 9:
Let ∠C be the smallest angle of ABC. Then, ∠A = 2∠C and B = 3∠C
Also, ∠A + ∠B + ∠C = 180o
⇒ 2∠C + 3∠C + ∠C = 180o
⇒ 6∠C = 180o
⇒ ∠C = 30o
So, ∠A = 2∠C = 2 (30o) = 60o
∠B = 3∠C = 3 (30o) = 90o
∴ The required angles of the triangle are 60o, 90o, 30o.
Question 10:
Let ABC be a right angled triangle and ∠C = 90o Since, ∠A + ∠B + ∠C = 180o
⇒ ∠A + ∠B = 180o – ∠C = 180o – 90o = 90o
Suppose ∠A = 53o
Then, 53o + ∠B = 90o
⇒ ∠B = 90o – 53o = 37o
∴ The required angles are 53o, 37o and 90o.
Question 11:
Let ABC be a triangle. Given, ∠A + ∠B = ∠C
We know, ∠A + ∠B + ∠C = 180o
⇒ ∠C + ∠C = 180o
⇒ 2∠C = 180o
⇒ ∠C =
![]()
= 90o
So, we find that ABC is a right triangle, right angled at C.
Question 12:
Given : ∆ABC in which ∠A = 90o, AL ⊥ BC To Prove: ∠BAL = ∠ACB
Proof :
In right triangle ∆ABC,
⇒ ∠ABC + ∠BAC + ∠ACB = 180o
⇒ ∠ABC + 90o + ∠ACB = 180o
⇒ ∠ABC + ∠ACB = 180o – 90o
∴ ∠ABC + ∠ACB = 90o
⇒ ∠ ACB = 90o – ∠ABC ….(1)
Similarly since ∆ABL is a right triangle, we find that,
∠BAL = 90o – ∠ABC …(2)
Thus from (1) and (2), we have
∴ ∠BAL = ∠ACB (Proved)
Question 13:
Let ABC be a triangle. So, ∠A < ∠B + ∠C
Adding A to both sides of the inequality,
⇒ 2∠A < ∠A + ∠B + ∠C
⇒ 2∠A < 180o
⇒ ∠A <
![]()
= 90o
[Since ∠A + ∠B + ∠C = 180o]
Similarly, ∠B < ∠A + ∠C
⇒ ∠B < 90o
and ∠C < ∠A + ∠B
⇒ ∠C < 90o
∆ABC is an acute angled triangle.
Question 14:
Let ABC be a triangle and ∠B > ∠A + ∠C Since, ∠A + ∠B + ∠C = 180o
⇒ ∠A + ∠C = 180o – ∠B Therefore, we get
∠B > 180o – ∠B
Adding ∠B on both sides of the inequality, we get,
⇒ ∠B + ∠B > 180o – ∠B + ∠B
⇒ 2∠B > 180o
⇒ ∠B >
![]()
= 90o
i.e., ∠B > 90o which means ∠B is an obtuse angle.
∆ABC is an obtuse angled triangle.
Question 15:
Since ∠ACB and ∠ACD form a linear pair. So, ∠ACB + ∠ACD = 180o
⇒ ∠ACB + 128o = 180o
⇒ ∠ACB = 180o – 128 = 52o
Also, ∠ABC + ∠ACB + ∠BAC = 180o
⇒ 43o + 52o + ∠BAC = 180o
⇒ 95o + ∠BAC = 180o
⇒ ∠BAC = 180o – 95o = 85o
∴ ∠ACB = 52o and ∠BAC = 85o.
Question 16:
As ∠DBA and ∠ABC form a linear pair. So, ∠DBA + ∠ABC = 180o
⇒ 106o + ∠ABC = 180o
⇒ ∠ABC = 180o – 106o = 74o
Also, ∠ACB and ∠ACE form a linear pair. So, ∠ACB + ∠ACE = 180o
⇒ ∠ACB + 118o = 180o
⇒ ∠ACB = 180o – 118o = 62o
In ∠ABC, we have,
∠ABC + ∠ACB + ∠BAC = 180o 74o + 62o + ∠BAC = 180o
⇒ 136o + ∠BAC = 180o
⇒ ∠BAC = 180o – 136o = 44o
∴ In triangle ABC, ∠A = 44o, ∠B = 74o and ∠C = 62o
Question 17:
(i) ∠EAB + ∠BAC = 180o [Linear pair angles]

110o + ∠BAC = 180o
⇒ ∠BAC = 180o – 110o = 70o
Again, ∠BCA + ∠ACD = 180o [Linear pair angles]
⇒ ∠BCA + 120o = 180o
⇒ ∠BCA = 180o – 120o = 60o
Now, in ∆ABC,
∠ABC + ∠BAC + ∠ACB = 180o
xo + 70o + 60o = 180o
⇒ x + 130o = 180o
⇒ x = 180o – 130o = 50o
∴ x = 50 (ii)
In ∆ABC,
∠A + ∠B + ∠C = 180o
⇒ 30o + 40o + ∠C = 180o
⇒ 70o + ∠C = 180o
⇒ ∠C = 180o – 70o = 110o
Now ∠BCA + ∠ACD = 180o [Linear pair]
⇒ 110o + ∠ACD = 180o
⇒ ∠ACD = 180o – 110o = 70o In ∆ECD,
⇒ ∠ECD + ∠CDE + ∠CED = 180o
⇒ 70o + 50o + ∠CED = 180o
⇒ 120o + ∠CED = 180o
∠CED = 180o – 120o = 60o
Since ∠AED and ∠CED from a linear pair So, ∠AED + ∠CED = 180o
⇒ xo + 60o = 180o
⇒ xo = 180o – 60o = 120o
∴ x = 120 (iii)
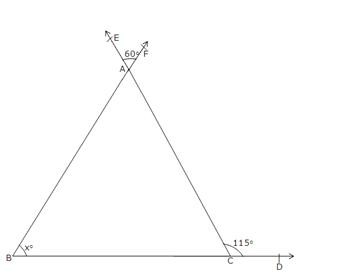
∠EAF = ∠BAC [Vertically opposite angles]
⇒ ∠BAC = 60o
In ∆ABC, exterior ∠ACD is equal to the sum of two opposite interior angles. So, ∠ACD = ∠BAC + ∠ABC
⇒ 115o = 60o + xo
⇒ xo = 115o – 60o = 55o
∴ x = 55 (iv)

Since AB || CD and AD is a transversal. So, ∠BAD = ∠ADC
⇒ ∠ADC = 60o
In ∠ECD, we have,
∠E + ∠C + ∠D = 180o
⇒ xo + 45o + 60o = 180o
⇒ xo + 105o = 180o
⇒ xo = 180o – 105o = 75o
∴ x = 75 (v)
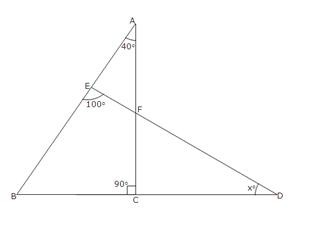
In ∆AEF,
Exterior ∠BED = ∠EAF + ∠EFA
⇒ 100o = 40o + ∠EFA
⇒ ∠EFA = 100o – 40o = 60o
Also, ∠CFD = ∠EFA [Vertically Opposite angles]
⇒ ∠CFD = 60o Now in ∆FCD,
Exterior ∠BCF = ∠CFD + ∠CDF
⇒ 90o = 60o + xo
⇒ xo = 90o – 60o = 30o
∴ x = 30 (vi)

In ∆ABE, we have,
∠A + ∠B + ∠E = 180o
⇒ 75o + 65o + ∠E = 180o
⇒ 140o + ∠E = 180o
⇒ ∠E = 180o – 140o = 40o
Now, ∠CED = ∠AEB [Vertically opposite angles]
⇒ ∠CED = 40o
Now, in ∆CED, we have,
∠C + ∠E + ∠D = 180o
⇒ 110o + 40o + xo = 180o
⇒ 150o + xo = 180o
⇒ xo = 180o – 150o = 30o
∴ x = 30
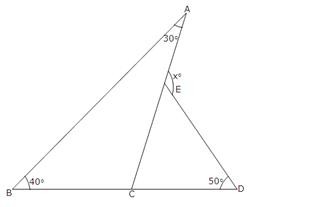
Question 18:

Produce CD to cut AB at E.
Now, in ∆BDE, we have,
Exterior ∠CDB = ∠CEB + ∠DBE
⇒ xo = ∠CEB + 45o In ∆AEC, we have,
…..(i)
Exterior ∠CEB = ∠CAB + ∠ACE
= 55o + 30o = 85o
Putting ∠CEB = 85o in (i), we get, xo = 85o + 45o = 130o
∴ x = 130
Question 19:
The angle ∠BAC is divided by AD in the ratio 1 : 3. Let ∠BAD and ∠DAC be y and 3y, respectively. As BAE is a straight line,
∠BAC + ∠CAE = 180o
[linear pair]
⇒ ∠BAD + ∠DAC + ∠CAE = 180o
⇒ y + 3y + 108o = 180o
⇒ 4y = 180o – 108o = 72o
⇒ y =
![]()
= 18o Now, in ∆ABC,
∠ABC + ∠BCA + ∠BAC = 180o
y + x + 4y = 180o
[Since, ∠ABC = ∠BAD (given AD = DB) and ∠BAC = y + 3y = 4y]
⇒ 5y + x = 180
⇒ 5 × 18 + x = 180
⇒ 90 + x = 180
∴ x = 180 – 90 = 90
Question 20:
Given : A ∆ABC in which BC, CA and AB are produced to D, E and F respectively. To prove : Exterior ∠DCA + Exterior ∠BAE + Exterior ∠FBD = 360o
Proof : Exterior ∠DCA = ∠A + ∠B ….(i) Exterior ∠FAE = ∠B + ∠C ….(ii) Exterior ∠FBD = ∠A + ∠C ….(iii) Adding (i), (ii) and (iii), we get,
Ext. ∠DCA + Ext. ∠FAE + Ext. ∠FBD
= ∠A + ∠B + ∠B + ∠C + ∠A + ∠C
= 2∠A + 2∠B + 2∠C
= 2 (∠A + ∠B + ∠C)
= 2 × 180o
[Since, in triangle the sum of all three angle is 180o]
= 360o
Hence, proved.
Question 21:
In ∆ACE, we have,
∠A + ∠C + ∠E = 180o ….(i) In ∆BDF, we have,
∠B + ∠D + ∠F = 180o ….(ii)
Adding both sides of (i) and (ii), we get,
∠A + ∠C +∠E + ∠B + ∠D + ∠F = 180o + 180o
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360o.
Question 22:
Given : In ∆ABC, bisectors of ∠B and ∠C meet at O and ∠A = 70o In ∆BOC, we have,
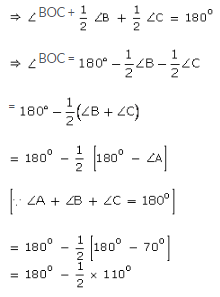
∠BOC + ∠OBC + ∠OCB = 180o
= 180o – 55o = 125o
∴ ∠BOC = 125o.
Question 23:
We have a ∆ABC whose sides AB and AC have been procued to D and E. A = 40o and bisectors of ∠CBD and ∠BCE meet at O.
In ∆ABC, we have, Exterior ∠CBD = C + 40o
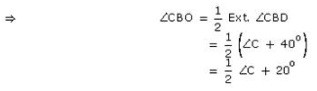
And exterior ∠BCE = B + 40o
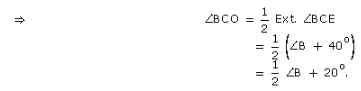
Now, in ∆BCO, we have,
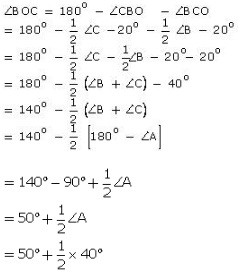
= 50o + 20o
= 70o
Thus, ∠BOC = 70o
Question 24:
In the given ∆ABC, we have,
∠A : ∠B : ∠C = 3 : 2 : 1
Let ∠A = 3x, ∠B = 2x, ∠C = x. Then,
∠A + ∠B + ∠C = 180o
⇒ 3x + 2x + x = 180o
⇒ 6x = 180o
⇒ x = 30o
∠A = 3x = 3 30o = 90o
∠B = 2x = 2 30o = 60o
and, ∠C = x = 30o
Now, in ∆ABC, we have,
Ext ∠ACE = ∠A + ∠B = 90o + 60o = 150o
∠ACD + ∠ECD = 150o
⇒ ∠ECD = 150o – ∠ACD
⇒ ∠ECD = 150o – 90o
⇒ ∠ECD= 60o
[since , AD ⊥ CD, ∠ACD = 90o]
Question 25:
In ∆ABC, AN is the bisector of ∠A and AM ⊥ BC. Now in ∆ABC we have;
∠A = 180o – ∠B – ∠C
⇒ ∠A = 180o – 65o – 30o
= 180o – 95o
= 85o
Now, in ∆ANC we have;

Thus, ∠MAN =
Question 26:
(i) False (ii) True (iii) False (iv) False (v) True (vi) True.